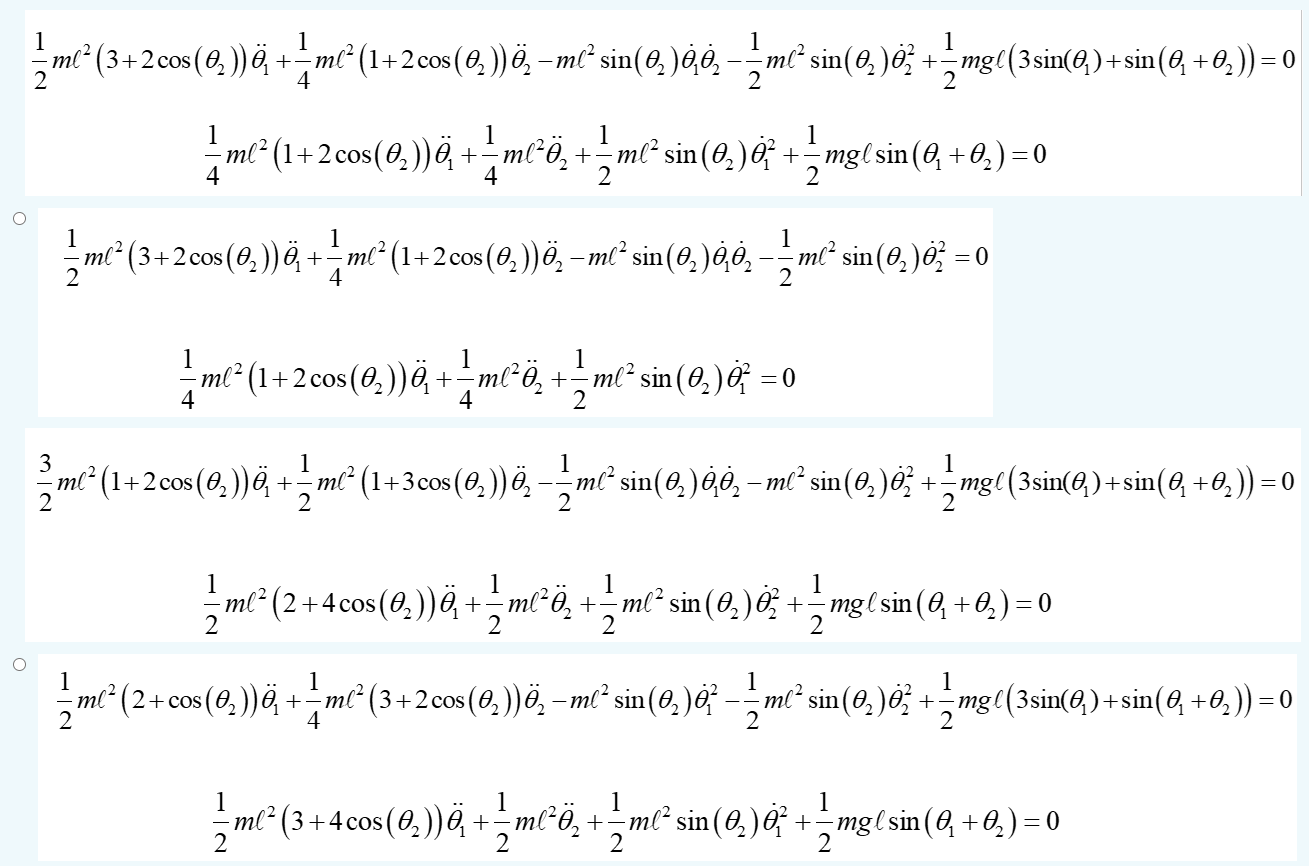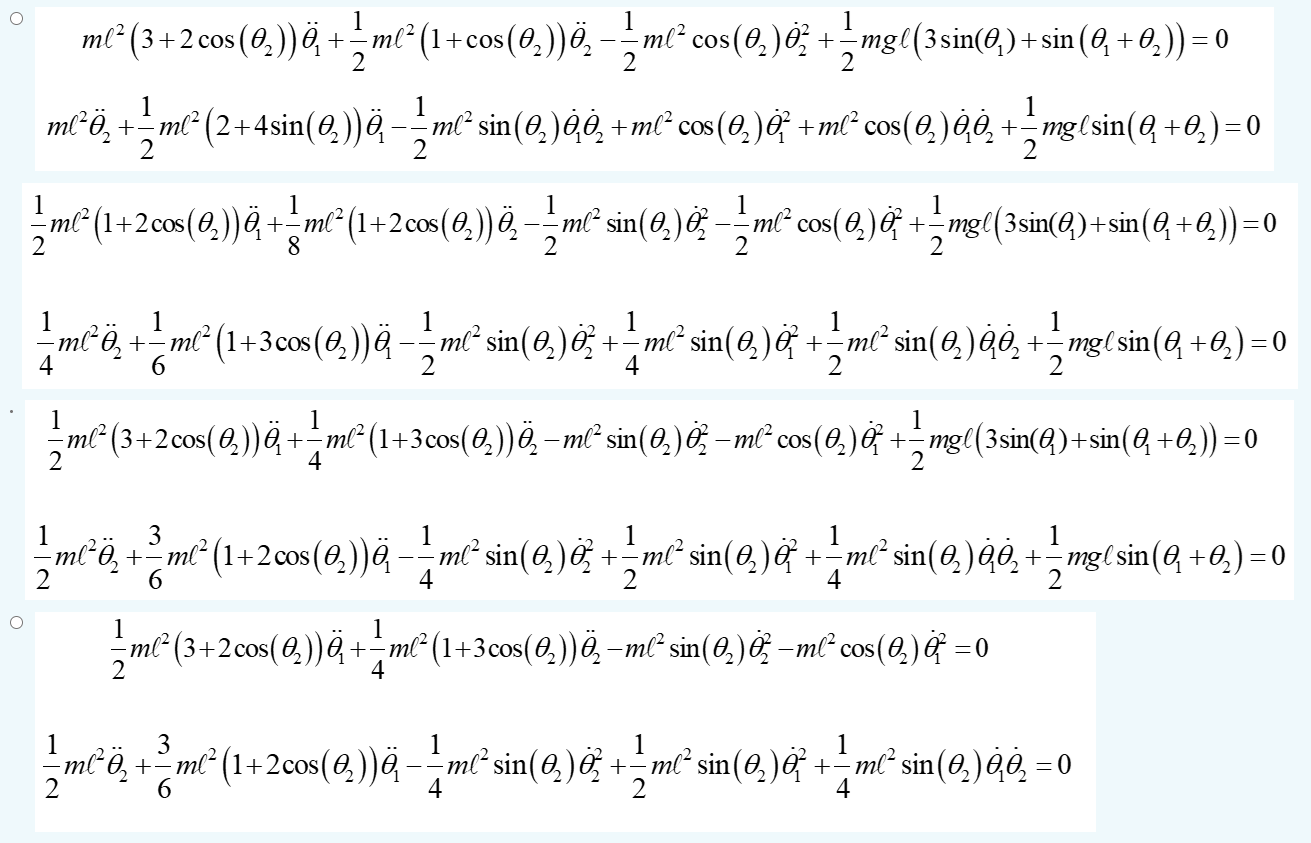(Solved): x Figure 1 illustrates a two-link planar robot manipulator. In this figure, and represent ...

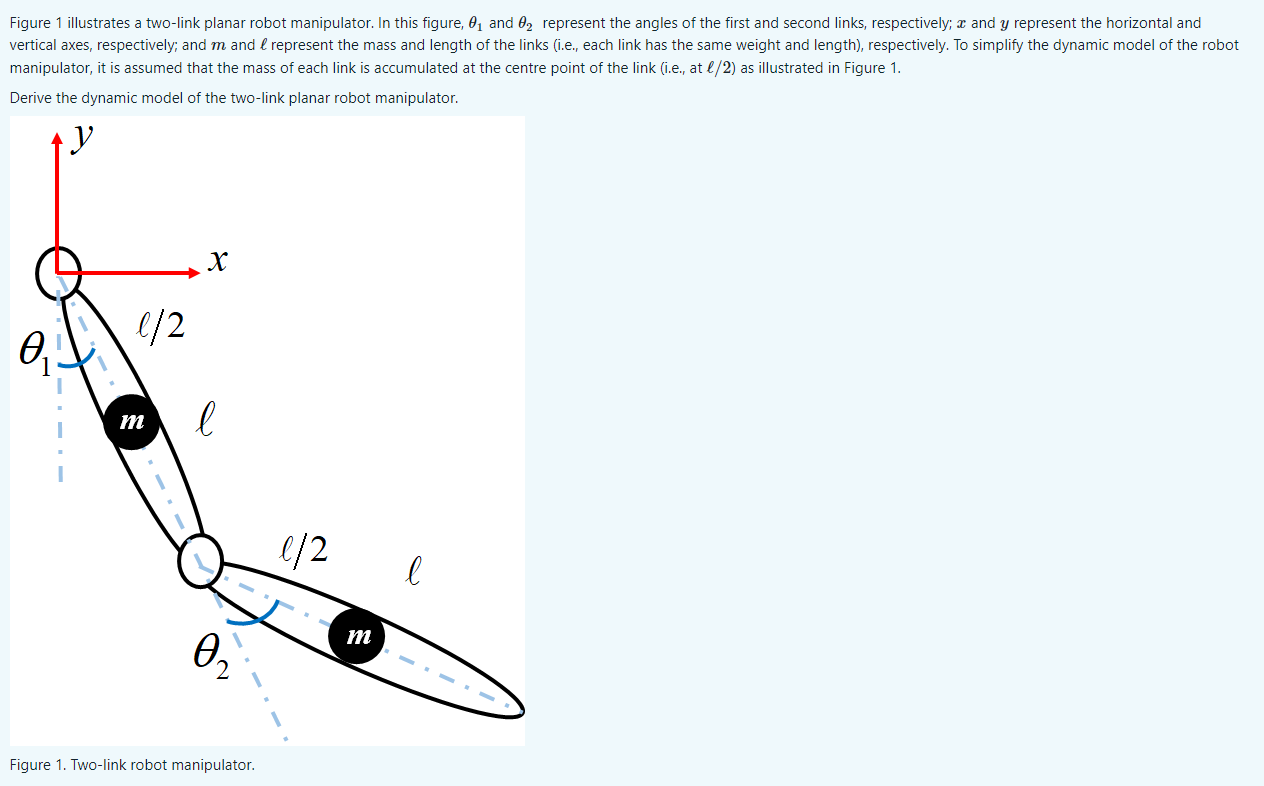
x Figure 1 illustrates a two-link planar robot manipulator. In this figure, ? and ? represent the angles of the first and second links, respectively; and y represent the horizontal and vertical axes, respectively; and m and represent the mass and length of the links (i.e., each link has the same weight and length), respectively. To simplify the dynamic model of the robot manipulator, it is assumed that the mass of each link is accumulated at the centre point of the link (i.e., at l/2) as illustrated in Figure 1. Derive the dynamic model of the two-link planar robot manipulator. X l/2 m ? 1/2 0? Figure 1. Two-link robot manipulator. m ? 1 ml² (3+2 cos (0,?)) Ï), + — ml² (1+2 cos (Q?)) Ï? — ml² sin(0?)?,?? ——_m²² sin(Q? )Ö³ +_mg{(3sin(Q) + sin(Q? +0,?)) = 0 2 4 2 1 1 1 me(1+2cos(0,) & t?m??i, tâm sin(0,)ê +?mg(sin(@ +0,) 0 = + +- 4 2 2 1 1 ml² (3+2 cos (0,?)) + m² (1+2 cos(0?))Ö¸ —m(² sin(0?)?‚Ö‚ Ï — — m² sin(0?)0³² = 0 4 1 1 m²² (1+2cos (0?)), + m{²0? + — m²² sin (0?)² = 0 1 ? ml 4 1 m²² (1+2cos (0?))) + — ml² (1+3 cos (0?)) ö? — — m²² sin(0?)??? – m²² sin(0?)0² + — mg{ (3sin(Q)) + sin(Q? +0,?)) = 0 2 1 1 1 ml² (2+4cos(0?))Ö), + — ml²Ö¸? + ½ ml² sin(0?)Ö³ +; +?mg(sin(0 +0,)=0 2 2 2 2 O 1 1 1 ml² (2+cos(0?))ä +_ml² (3+2 cos (0?)) ö? ?ml² sin(0?)?² — — ml² sin (0?)0² + mgl (3sin(0?)+sin(Q? +0?2)) = 0 4 2 1 1 1 ml² (3+4 cos (0?)) Ö? + ?ml²Ö? + ?ml² sin (0?) 0² + ? mgl sin ( 0? +0? ) = 0 +?mg(sin(@,+0,)=0 2 2 2 O O 1 1 ml² (3+2 cos (0?)) + - ml² (1+cos (0?))Ö? — — ml³² cos(0?)² + — mg ((3 sin(0?) + sin(0? +0,?)) = 0 Ï - 2 2 1 1 ml²Ö? + ? ml² (2+4sin(Q?))Ö —— ml² sin (O?)Ò‚ª? + ml² cos (0?)²³ +ml² cos(Q?)ÒÒ? +? mg(sin(Q +0? ) = 0 2 2 2 1 1 ml² (1+2cos (0,?)) Ï‚ + ¹m²² (1+2cos (0?)) Ï‚ — ¹m²² sin(0?) - ¹ m² cos(0?) +-¹mgl (3sin(Q?)+sin(0, +0?)) = 0 2 8 1 1 1 1 1 - m², + ¹m² (1 + 3 cos (9?))m²² sin(0,), + m² sin(0,)& + m²^² sin(0?)??? + ¹ mgl sin(Q? + 0,?)=0 4 6 4 2 2 1 1 - m² (3+2 cos(Q))Q+= m(²(1+3coss(Q?))Ö – m² sin(Q?)Œ – m² coss (0?) Œ +½mg!((3sin(Q)+sin(Q+Q?)) 0 2 4 1 3 1 1 1 ¹ ml²Ö? + — ml² (1+2 cos (?)) m sin(0,) +=msin(0,)ê + \msin(0,)40,+=mg(sin(4 +0,)=0 4 O 1 - ml² (3 + 2 cos(6?)) + _ m² (1 + 3 cos (0,?)) ä¸ _ml² sin(4?) &, _m² cos(0?) € = 0 4 1 3 1 1 _m(²0? + ² ml² (1+2cos (0?))Ö — — ml² sin(0?)¤ + - ml² sin(0?)0² + ?ml² sin(0?)?ª? = 0 4