(Solved): Write a system of four equations whose solution gives estimates for the temperatures \( T_{1}, T_{ ...

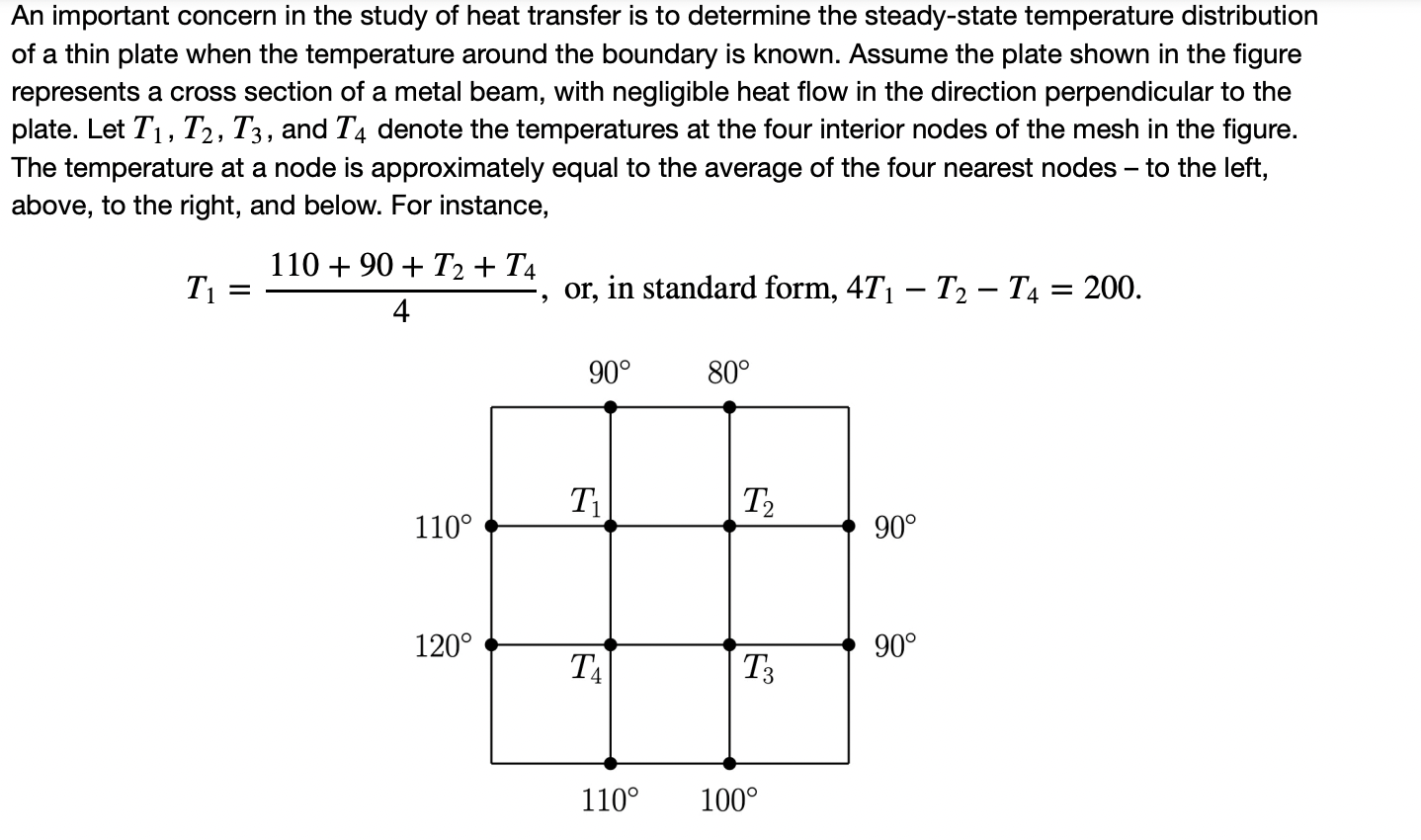
Write a system of four equations whose solution gives estimates for the temperatures \( T_{1}, T_{2}, T_{3} \), and \( \mathrm{T}_{4} \). Set up an augmented matrix associated to the system of equations. Use Gauss-Jordan elimination to solve the system of equations and find values for \( T_{1}, T_{2}, T_{3} \), and \( T_{4} \). Carefully and clearly show your intermediate steps. An important concern in the study of heat transfer is to determine the steady-state temperature distribution of a thin plate when the temperature around the boundary is known. Assume the plate shown in the figure represents a cross section of a metal beam, with negligible heat flow in the direction perpendicular to the plate. Let \( T_{1}, T_{2}, T_{3} \), and \( T_{4} \) denote the temperatures at the four interior nodes of the mesh in the figure. The temperature at a node is approximately equal to the average of the four nearest nodes - to the left, above, to the right, and below. For instance, \[ T_{1}=\frac{110+90+T_{2}+T_{4}}{4}, \text { or, in standard form, } 4 T_{1}-T_{2}-T_{4}=200 \]