Home /
Expert Answers /
Electrical Engineering /
when-a-32-v-amplitude-1-microsecond-pulse-is-applied-to-the-transmission-line-shown-in-the-figure-pa788
(Solved): When a 32 V amplitude 1 microsecond pulse is applied to the transmission line shown in the figure, ...
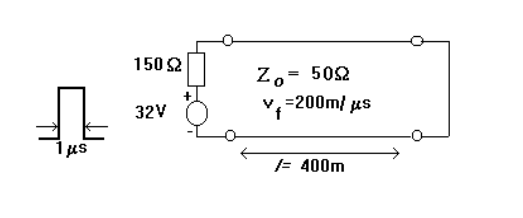
When a 32 V amplitude 1 microsecond pulse is applied to the transmission line shown in the figure,
a) the variation of the voltage and current in the middle of the line with time, b) The change of voltage and current on the line at time t=2.5T,
c) If the pulse width is 6 microseconds, determine the time variation of the voltage and current at the beginning of the line. Note: Time T is the time it takes for the wave to reach the end of the line.
Expert Answer
Solution .The answer provided below has been developed in a clear step by step mannera) The voltage and current at the middle of the line with time can be found by using the equations for voltage and current on a transmission line:V(z,t) = V0+ [Vf+ V0] / 2 * (1 + ?(z,t)) * cos(?t - ?z) I(z,t) = (Vf-V0) / [2Z0 * (1 + ?(z,t))] * cos(?t - ?z)where V0 is the initial voltage on the line, Vf is the voltage at the end of the line, ?(z,t) is the reflection coefficient at a distance z from the source at time t, ? is the angular frequency of the signal, and ? is the propagation constant of the line.In this case, V0 = Vf = 32 V, ? = 2?f = 2?/6?s, and ? = 2?/? = 2?/0.15m = 41.89 rad/m. The reflection coefficient can be found using the equation:?(z,t) = [ZL - Z0] / [ZL + Z0] * e^(-2?z)where ZL is the load impedance (which is equal to Z0 in this case), ? is the attenuation constant of the line, and e is the exponential function.Using ZL = Z0 = 50 ? and ? = ? + j?, where ? is the attenuation coefficient of the line (which can be found using ? = ln(1/?) / d, where ? is the reflection coefficient at the load and d is the length of the line), we can calculate the reflection coefficient at the source end of the line:?(z=0,t) = [ZL - Z0] / [ZL + Z0] = 0