(Solved): What is the second degree coefficient of the Taylor series of \( f(x)=\ln (3 x+1) \) centered at \( ...

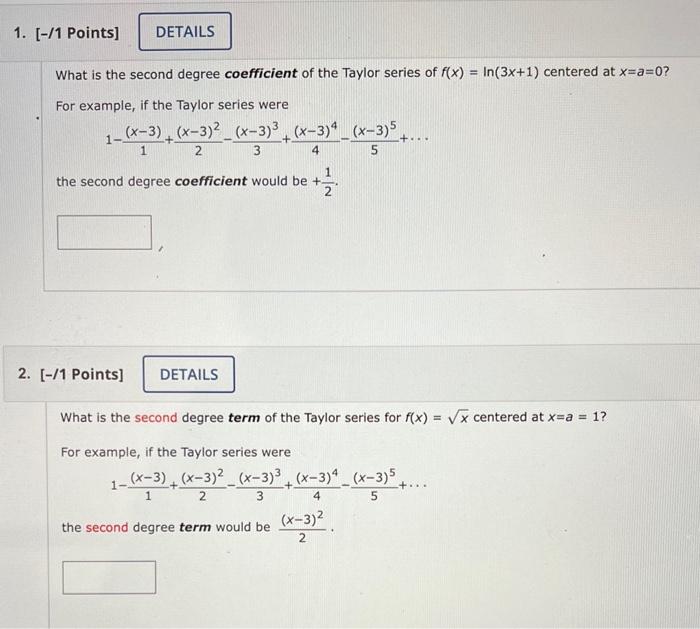
What is the second degree coefficient of the Taylor series of \( f(x)=\ln (3 x+1) \) centered at \( x=a=0 \) ? For example, if the Taylor series were \[ 1-\frac{(x-3)}{1}+\frac{(x-3)^{2}}{2}-\frac{(x-3)^{3}}{3}+\frac{(x-3)^{4}}{4}-\frac{(x-3)^{5}}{5}+\cdots \] the second degree coefficient would be \( +\frac{1}{2} \). [-11 Points] What is the second degree term of the Taylor series for \( f(x)=\sqrt{x} \) centered at \( x=a=1 \) ? For example, if the Taylor series were \[ 1-\frac{(x-3)}{1}+\frac{(x-3)^{2}}{2}-\frac{(x-3)^{3}}{3}+\frac{(x-3)^{4}}{4}-\frac{(x-3)^{5}}{5}+\cdots \] the second degree term would be \( \frac{(x-3)^{2}}{2} \).