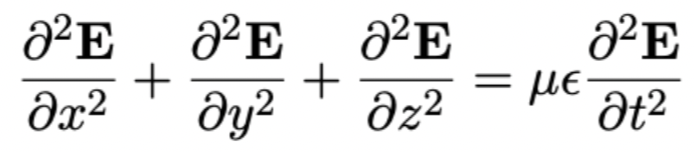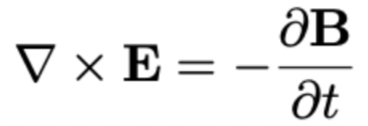(Solved): WAVE EQUATION: FARADAY'S LAW: Let \( \mathbf{E}=\hat{x} E_{x}(z, t) \) where \( E_{x}(z, t)=E_{0 ...

WAVE EQUATION:

FARADAY'S LAW:

Let \( \mathbf{E}=\hat{x} E_{x}(z, t) \) where \( E_{x}(z, t)=E_{0} \cos (\omega t \mp \beta z+\phi) \) and \( E_{0} \) (amplitude), \( \omega \) (angular frequency), \( \beta \) (wavenumber), and \( \phi \) (phase shift) are positive real scalars. These fields describe wave polarized in the \( \hat{x} \) direction and propagating in the \( \pm \hat{z} \) direction, respectively. a) Show that the specified \( E_{x} \) satisfies the wave equation derived above if: \[ \beta=\omega \sqrt{\mu_{0} \epsilon_{0}}=\frac{\omega}{c} \] where \( c \approx 3 \times 10^{8} \mathrm{~m} / \mathrm{s} \) is the speed of light in free space. b) Substitute the specified \( E_{x} \) into Faraday's law and solve for \( \mathbf{B}(z, t) \) assuming that \( \mathbf{B}(0,0)= \) \( \pm \frac{E_{x}(0,0)}{c} \hat{y} \). Show that your answer can be expressed as \( \mathbf{B}=\pm \frac{E_{x}}{c} \hat{y} \) (be careful about maintaining the correct order for the upper and lower signs). Are there any restrictions on the value for \( \phi \) ? \( \frac{\partial^{2} \mathbf{E}}{\partial x^{2}}+\frac{\partial^{2} \mathbf{E}}{\partial y^{2}}+\frac{\partial^{2} \mathbf{E}}{\partial z^{2}}=\mu \epsilon \frac{\partial^{2} \mathbf{E}}{\partial t^{2}} \) \( \nabla \times \mathbf{E}=-\frac{\partial \mathbf{B}}{\partial t} \)