(Solved): v 2. 30 marks An open-top trough can be constructed by bending a rectangular sheet of metal of width ...

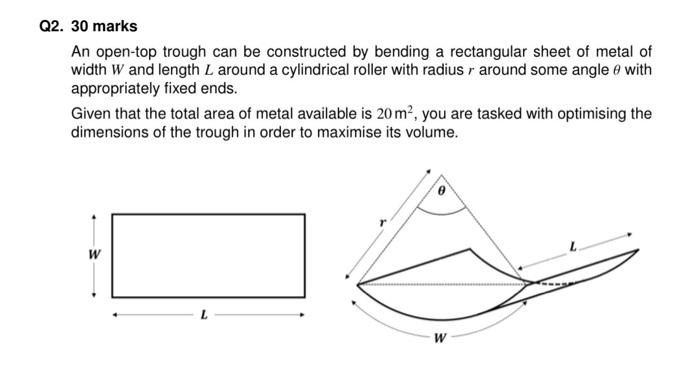
2. 30 marks An open-top trough can be constructed by bending a rectangular sheet of metal of width \( W \) and length \( L \) around a cylindrical roller with radius \( r \) around some angle \( \theta \) with appropriately fixed ends. Given that the total area of metal available is \( 20 \mathrm{~m}^{2} \), you are tasked with optimising the dimensions of the trough in order to maximise its volume. \[ \begin{aligned} V &=\frac{1}{2} r^{2} L(\theta-\sin \theta) \\ 20 \mathrm{~m}^{2} &=r \theta L+r^{2}(\theta-\sin \theta) \end{aligned} \] [5 marks] (b) Given the equations in part (a), use the Lagrange method of constrained optimisation, to represent the problem as a system of equations (i.e. make use of \( \nabla f=\lambda \nabla g \). [6 marks] (c) Solve the system of equations to determine the dimensions of the trough (i.e. the values of \( L, r \), and \( \theta \) ) which maximise its volume. Hint: \( \operatorname{try} \theta=\pi \). [5 marks]