(Solved): Using the substitution u=sec^(-1)((x)/(3)), we obtain \int (x^(2))/(\sqrt(x^(2)-9))dx=\int Ksec^(m)u ...

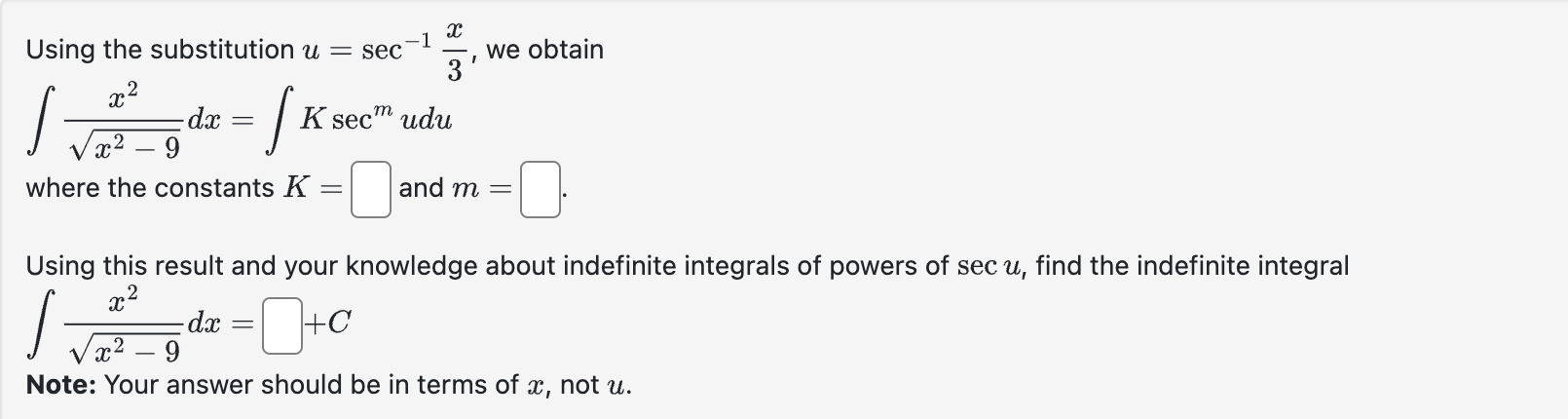
Using the substitution u=sec^(-1)((x)/(3)), we obtain \int (x^(2))/(\sqrt(x^(2)-9))dx=\int Ksec^(m)udu where the constants K= and m= Using this result and your knowledge about indefinite integrals of powers of secu, find the indefinite integral \int (x^(2))/(\sqrt(x^(2)-9))dx=,+C Note: Your answer should be in terms of x, not u.