(Solved): Using the Biot-Savart law for a bound surface current \[ \vec{B}=\frac{\mu_{0 ...

???????

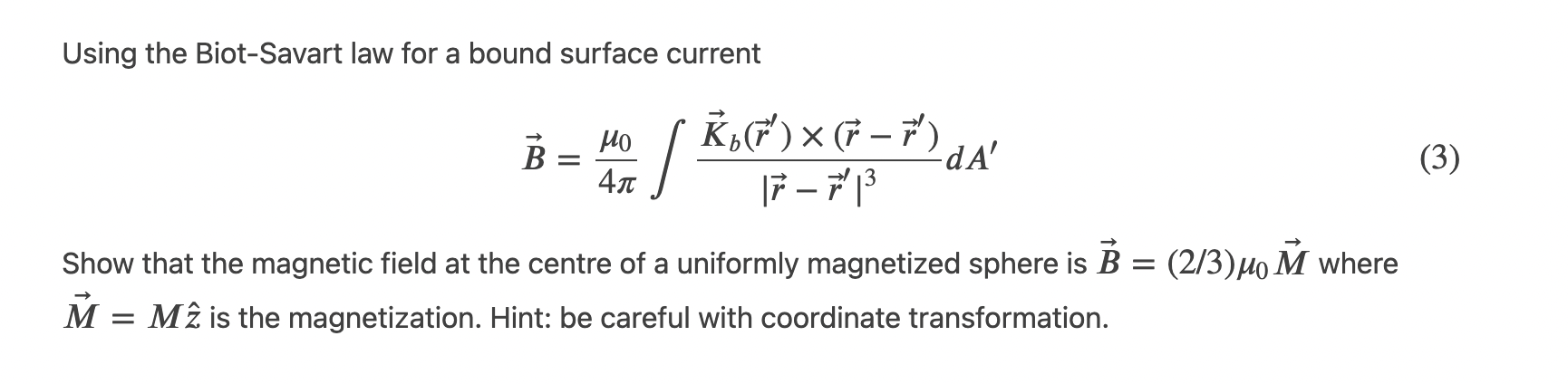
Using the Biot-Savart law for a bound surface current \[ \vec{B}=\frac{\mu_{0}}{4 \pi} \int \frac{\vec{K}_{b}\left(\vec{r}^{\prime}\right) \times\left(\vec{r}-\vec{r}^{\prime}\right)}{\left|\vec{r}-\vec{r}^{\prime}\right|^{3}} d A^{\prime} \] Show that the magnetic field at the centre of a uniformly magnetized sphere is \( \vec{B}=(2 / 3) \mu_{0} \vec{M} \) where \( \vec{M}=M \hat{z} \) is the magnetization. Hint: be careful with coordinate transformation.