(Solved): Using R, construct side-by-side box plots for the two sets of data below. Data Set 1: \[ \begin{arr ...

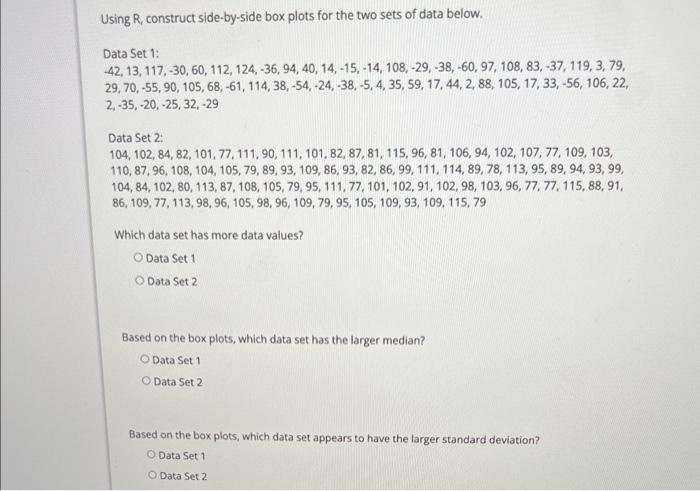
Using R, construct side-by-side box plots for the two sets of data below. Data Set 1: \[ \begin{array}{l} -42,13,117,-30,60,112,124,-36,94,40,14,-15,-14,108,-29,-38,-60,97,108,83,-37,119,3,79, \\ 29,70,-55,90,105,68,-61,114,38,-54,-24,-38,-5,4,35,59,17,44,2,88,105,17,33,-56,106,22 \\ 2,-35,-20,-25,32,-29 \end{array} \] Data Set 2: \[ \begin{array}{l} 104,102,84,82,101,77,111,90,111,101,82,87,81,115,96,81,106,94,102,107,77,109,103, \\ 110,87,96,108,104,105,79,89,93,109,86,93,82,86,99,111,114,89,78,113,95,89,94,93,99 \text {, } \\ 104,84,102,80,113,87,108,105,79,95,111,77,101,102,91,102,98,103,96,77,77,115,88,91 \text {, } \\ 86,109,77,113,98,96,105,98,96,109,79,95,105,109,93,109,115,79 \end{array} \] Which data set has more data values? Data Set 1 Data Set 2 Based on the boxplots, which data set has the larger median? Data Set 1 Data Set 2 Based on the box plots, which data set appears to have the larger standard deviation? Data Set 1 Data Set 2 Forty-five graduating students at a local community college were surveyed to find their age upon graduation. \[ \begin{array}{l} 64,59,30,57,25,21,58,32,23,23,63,21,32,55,61,28,30,22,25,24,30,24,28,30,32,24,24,25, \\ 31,22,24,23,23,22,24,57,24,26,21,62,24,22,24,26,25 \end{array} \] Find the 59 th percentile of the data. years Use R to construct a boxplot for the data below. \[ \begin{array}{l} 196.1,167.6,158.8,159.5,159.3,119.2,191.8,158.9,52.6,62.2,46,72.8,162.9,65.4,168.3,159.8 \\ 99,62.1,188.8,139.8,129.7,47.7,41.1,133.2,132.3,188.6,185.2,196.7,173.6,134.2,167.6,159.7, \\ 158,64.4,149,103.8,53.3,160.4,129.2,119.6,89.5,78,193.1,146.3,90,142.2,167.4,159.2,40, \\ 118.9,161.5,174.4,41.1,43,163,127.9,89.6,161.3,66.4,65.7,63.6,197.7,57.6,52.5,97.9,198.1 \text {, } \\ 53.2,161.3,159,194,199.9,196.1,159.7,161.9,81.4,173.5,128.1,68.1,177.3,181.9,141.6,191.2 \\ 76.8,176.7,162.2,41.2,158.8,54.1,68.2,203,160.7,160.6,158,187.1,158.6,158.2,157.5,44.6 \\ 50.2,183.9,75.3,163,159.2,164.5,158,162.7,51.7,164.7,138,160.9,144.9,130.7,158,59.1,125.4, \\ 93.1,167.4 \end{array} \] Which quarter has the smallest spread of data? The quarter between the minimum value and \( Q_{1} \). The quarter between \( Q_{1} \) and \( Q_{2} \). The quarter between \( Q_{2} \) and \( Q_{3} \). The quarter between \( Q_{3} \) and the maximum value. The quarters all have the same spread of data. It's impossible to tell which quarter has the smallest spread. Which quarter has the largest spread of data? The quarter between the minimum value and \( Q_{1} \). The quarter between \( Q_{1} \) and \( Q_{2} \). The quarter between \( Q_{2} \) and \( Q_{3} \). The quarter between \( Q_{3} \) and the maximum value. The quarters all have the same spread of data. it's impossible to tell which quarter has the largest spread.