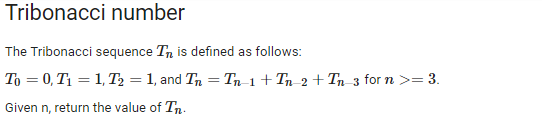(Solved): Using Python Please Tribonacci number The Tribonacci sequence \( T_{n} \) is defined as follows ...

Using Python Please

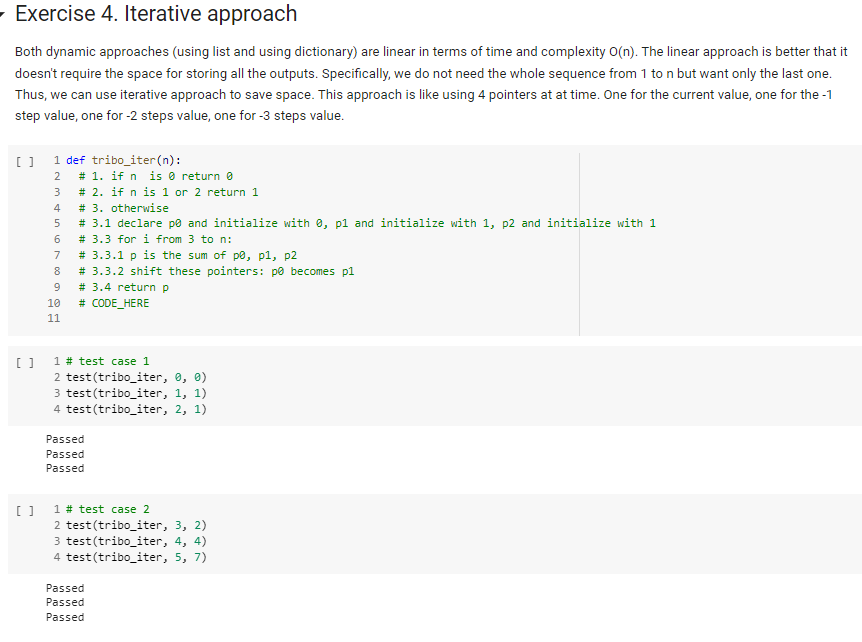
Tribonacci number The Tribonacci sequence \( T_{n} \) is defined as follows: \( T_{0}=0, T_{1}=1, T_{2}=1 \), and \( T_{n}=T_{n-1}+T_{n-2}+T_{n-3} \) for \( n>=3 \). Given \( n \), return the value of \( T_{n} \). Exercise 4. Iterative approach Both dynamic approaches (using list and using dictionary) are linear in terms of time and complexity \( \mathrm{O}(\mathrm{n}) \). The linear approach is better that it doesn't require the space for storing all the outputs. Specifically, we do not need the whole sequence from 1 to \( n \) but want only the last one. Thus, we can use iterative approach to save space. This approach is like using 4 pointers at at time. One for the current value, one for the -1 step value, one for \( -2 \) steps value, one for \( -3 \) steps value. [ ] 1 \# test case 1 2 test(tribo_iter, 0,0 ) 3 test(tribo_iter, 1,1) 4 test(tribo_iter, 2,1) Passed Passed Passed [ ] 1 \# test case 2 2 test(tribo_iter, 3, 2) 3 test(tribo_iter, 4, 4) 4 test(tribo_iter, 5, 7) Passed Passed Passed