(Solved): use the worked out quaratic equation and NOT thr given one \r\n\r\nii. Create detailed pseudo code ...

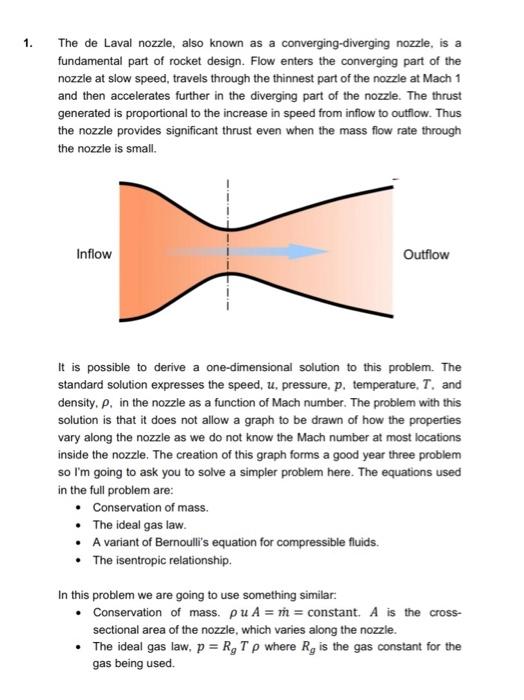
\r\n\r\nii. Create detailed pseudo code for the algorithm. If you have been unable to derive the quadratic equation for density assume it is: \\[ R_{g} T \\rho^{2}-p_{T} \\rho+(\\dot{m})^{2} / A=0 \\]\r\n\r\n1. The de Laval nozzle, also known as a converging-diverging nozzle, is a fundamental part of rocket design. Flow enters the converging part of the nozzle at slow speed, travels through the thinnest part of the nozzle at Mach 1 and then accelerates further in the diverging part of the nozzle. The thrust generated is proportional to the increase in speed from inflow to outflow. Thus the nozzle provides significant thrust even when the mass flow rate through the nozzie is small. It is possible to derive a one-dimensional solution to this problem. The standard solution expresses the speed, \\( u \\), pressure, \\( p \\), temperature, \\( T \\), and density, \\( \\rho \\), in the nozzle as a function of Mach number. The problem with this solution is that it does not allow a graph to be drawn of how the properties vary along the nozzle as we do not know the Mach number at most locations inside the nozzle. The creation of this graph forms a good year three problem so l'm going to ask you to solve a simpler problem here. The equations used in the full problem are: - Conservation of mass. - The ideal gas law. - A variant of Bernoulli's equation for compressible fluids. - The isentropic relationship. In this problem we are going to use something similar: - Conservation of mass. \\( \\rho u A=m= \\) constant. \\( A \\) is the crosssectional area of the nozzle, which varies along the nozzle. - The ideal gas law, \\( p=R_{g} T \\rho \\) where \\( R_{g} \\) is the gas constant for the gas being used.\r\n- The incompressible form of Bernoulli's equation, \\( 0.5 \\rho u^{2}+p=p_{T}= \\) constant - Temperature is constant. This equation set is not consistent, but it simplifies the problem. The values of the temperature, speed and pressure are known at the inflow. The variation of area with distance along the nozzle is also known. The challenge is to plot graphs of how the speed, pressure and density varies along the nozzle. The radius of the nozzle, which has a circular cross section, is given as a function of distance along the nozzle, \\( x \\),.by the equation: \\[ r=0.01+0.05 * \\cos \\left(\\pi\\left(\\frac{x}{0.08}\\right)^{0.6}\\right) \\quad 0