(Solved): Use the Law of Sines to find the indicated side \( x \). (Assume \( a=17 \). Round your answer to ...

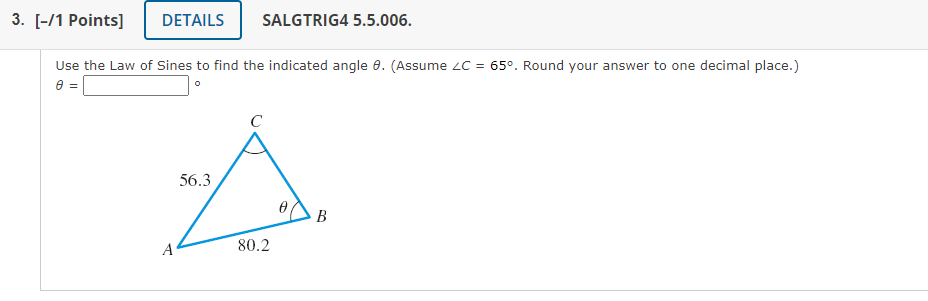
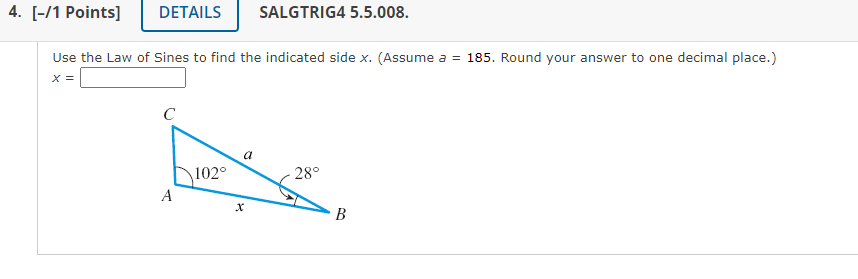
Use the Law of Sines to find the indicated side \( x \). (Assume \( a=17 \). Round your answer to one decimal place.) \[ x= \] Use the Law of Sines to find the indicated angle \( \theta \). (Assume \( \angle C=65^{\circ} \). Round your answer to one decimal place.) \( \theta= \) Use the Law of Sines to find the indicated side \( x \). (Assume \( a=185 \). 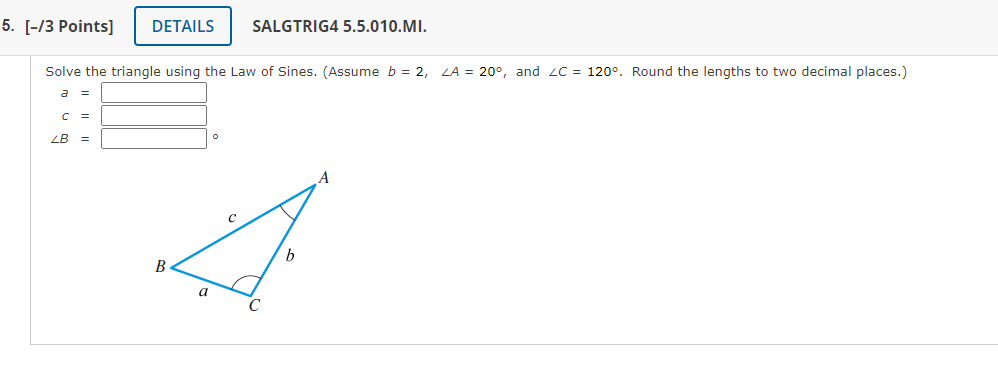Round your answer to one decimal place.) \[ x= \] Solve the triangle using the Law of Sines. (Assume \( b=2, \angle A=20^{\circ} \), and \( \angle C=120^{\circ} \). 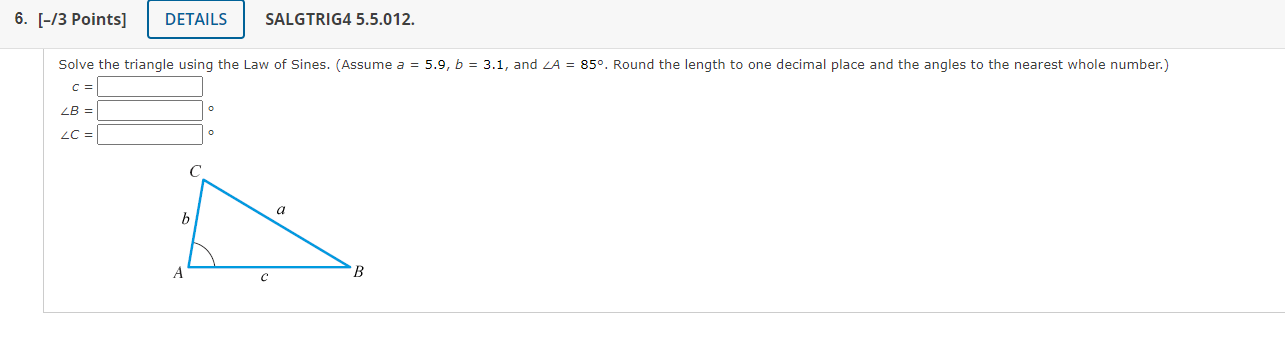Round the lengths to two decimal places.) \[ \begin{aligned} a &=\\ c &=\\ \angle B &= \end{aligned} \] Solve the triangle using the Law of Sines. (Assume \( a=5.9, b=3.1 \), and \( \angle A=85^{\circ} \). Round the length to one decimal place and the angles to the nearest whole number.) \( c= \) \[ \angle B=\quad \circ \] \[ \angle C=\quad \quad \circ \] Sketch the triangle. \[ \angle A=25^{\circ}, \quad \angle B=95^{\circ}, \quad C=70 \] Solve the triangle using the Law of Sines. (Round side lengths to one decimal place.) \( a= \) \[ b= \] \[ \angle C= \] \[ \angle A=24^{\circ}, \quad \angle B=110^{\circ}, \quad a=450 \] Solve the triangle using the Law of Sines. (Round side lengths to one decimal place.) \[ b= \] \[ c=1 \] \[ \angle C= \] Sketch the triangle. \[ \angle B=12^{\circ}, \quad \angle C=99^{\circ}, \quad C=105 \] Solve the triangle using the Law of Sines. (Round side lengths to the nearest integer.) \[ \begin{aligned} a &=\\ b &=\\ \angle A &= \end{aligned} \] 0. [-/6 Points \( ] \) SALGTRIG4 5.5.020.MI. 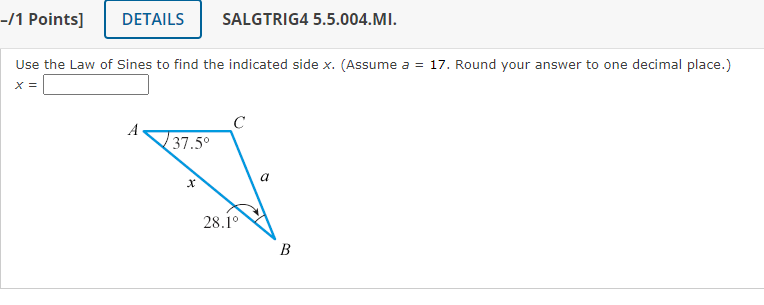\( a=31, \quad c=46, \quad \angle A=31^{\circ} \) \( b=45, \quad c=44, \quad \angle C=31^{\circ} \) \begin{tabular}{l|ll|l} \( \angle A_{1}= \) & \( 1 \circ \) & \( \angle A_{2}= \) & \\ \( \angle B_{1}= \) & \( \circ \) & \( \angle B_{2}= \) & \( \circ \) \end{tabular} [-/6 Points] \( \quad \) SALGTRIG4 5.5.024. \( a=77, \quad b=106, \quad \angle A=26^{\circ} \)