Home /
Expert Answers /
Calculus /
use-the-divergence-theorem-to-calculate-the-surface-integral-nbsp-nbsp-pa697
(Solved): Use the Divergence Theorem to calculate the surface integral ...
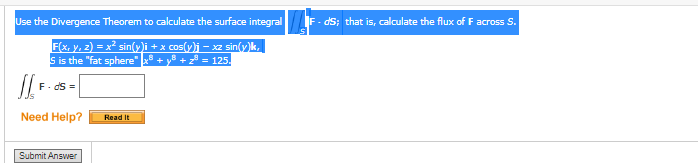
Use the Divergence Theorem to calculate the surface integral
| S |
F · dS;
that is, calculate the flux of F across S.
F(x, y, z) = x2 sin(y)i + x cos(y)j ? xz sin(y)k,
S is the "fat sphere"
x8 + y8 + z8 = 125.
\( \mathrm{F}(x, y, z)=x^{2} \sin (y) i+x \cos (y) i-x z \sin (y) \boldsymbol{k}, \mid \) \( S \) is the "fat sphere " \( x^{8}+y^{8}+z^{8}=125 \). \( \iint_{S} \mathrm{~F} \cdot d S= \)
Expert Answer
Given: F(x,y,z)=x2sin?yi^+x