(Solved): Use a \( 0.05 \) level of significance to test whether the temperature level has an effect on the ...

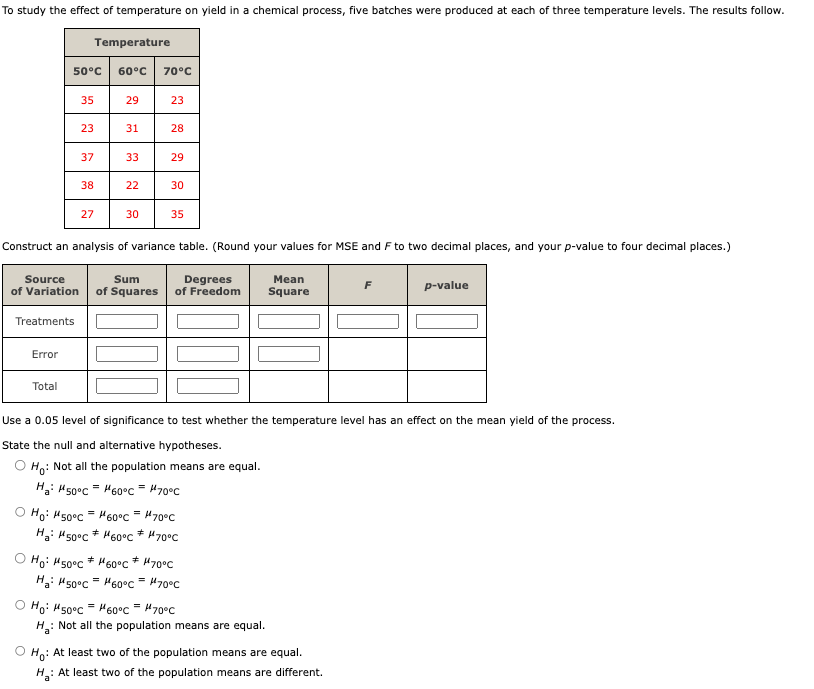
Use a \( 0.05 \) level of significance to test whether the temperature level has an effect on the mean yield of the process. State the null and alternative hypotheses. \( H_{0} \) : Not all the population means are equal. \[ \begin{array}{l} H_{a}: \mu_{50^{\circ} \mathrm{C}}=\mu_{60^{\circ} \mathrm{C}}=\mu_{70^{\circ}} \mathrm{C} \\ H_{0}: \mu_{50^{\circ} \mathrm{C}}=\mu_{60^{\circ} \mathrm{C}}=\mu_{70^{\circ} \mathrm{C}} \\ H_{a}: \mu_{50^{\circ} \mathrm{C}} \neq \mu_{60^{\circ} \mathrm{C}} \neq \mu_{70^{\circ} \mathrm{C}} \\ H_{0}: \mu_{50^{\circ} \mathrm{C}} \neq \mu_{60^{\circ} \mathrm{C}} \neq \mu_{70^{\circ} \mathrm{C}} \\ H_{\mathrm{a}}: \mu_{50^{\circ} \mathrm{C}}=\mu_{60^{\circ} \mathrm{C}}=\mu_{70^{\circ}} \mathrm{C} \\ H_{0}: \mu_{50^{\circ} \mathrm{C}}=\mu_{60^{\circ} \mathrm{C}}=\mu_{70^{\circ} \mathrm{C}} \\ H_{a}: \text { Not all the population means are equal. } \\ H_{0}: \text { At least two of the population means are equal. } \\ H_{a}: \text { At least two of the population means are different. } \end{array} \] Find the value of the test statistic. (Round your answer to two decimal places.) Find the \( \rho \)-value. (Round your answer to four decimal places.) \( p \)-value \( = \) State your conclusion. Do not reject \( H_{0} \). There is not sufficient evidence to conclude that the mean yields for the three temperatures are not equal. Do not reject \( H_{0} \). There is sufficient evidence to conclude that the mean yields for the three temperatures are not equal. Reject \( H_{0} \). There is not sufficient evidence to conclude that the mean yields for the three temperatures are not equal. Reject \( H_{0} \). There is sufficient evidence to conclude that the mean yields for the three temperatures are not equal.