Home /
Expert Answers /
Physics /
three-different-objects-all-with-different-masses-are-initially-at-rest-at-the-bottom-of-a-set-of-pa771
(Solved): Three different objects, all with different masses, are initially at rest at the bottom of a set of ...
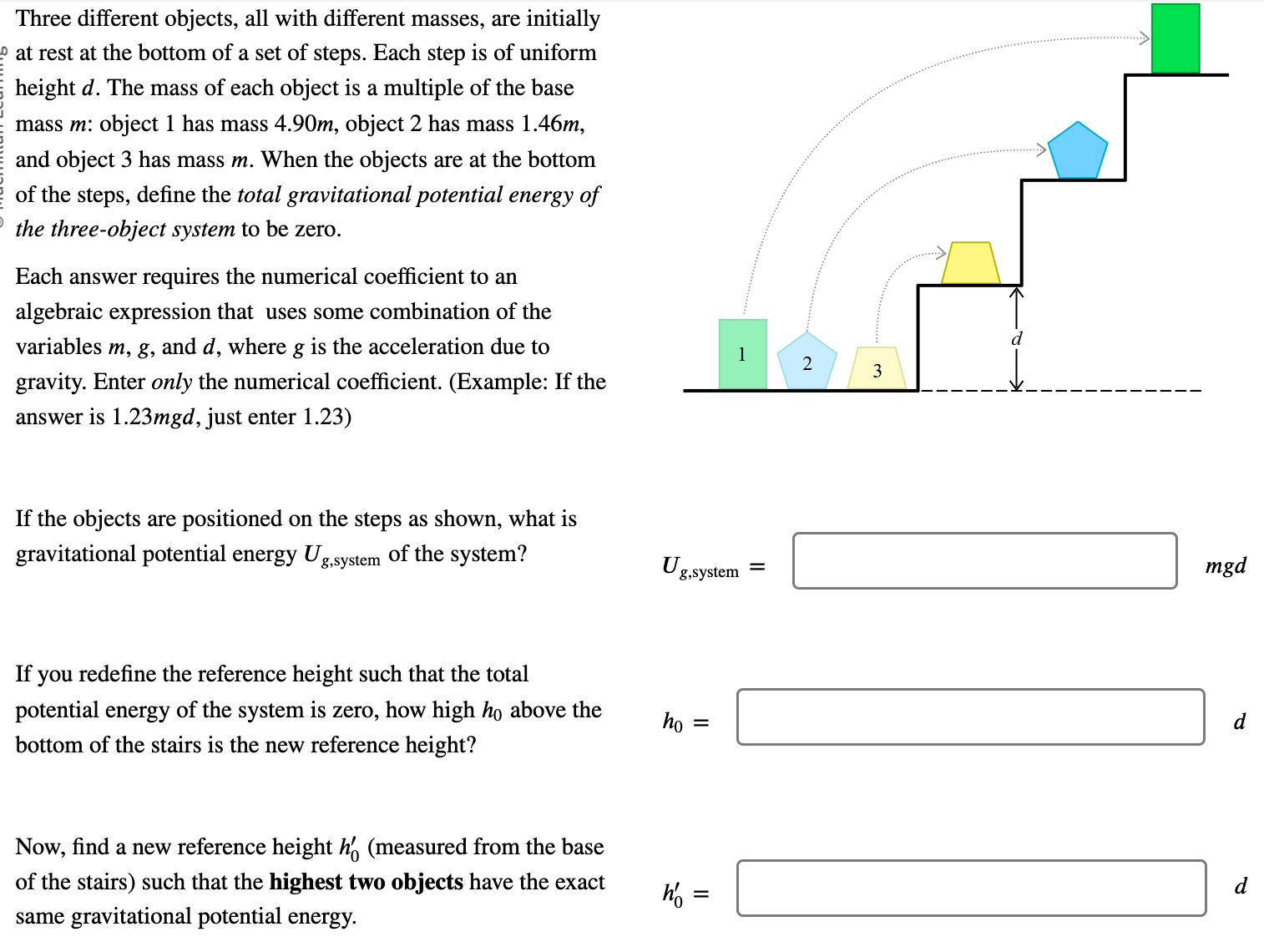
Three different objects, all with different masses, are initially at rest at the bottom of a set of steps. Each step is of uniform height . The mass of each object is a multiple of the base mass : object 1 has mass , object 2 has mass , and object 3 has mass . When the objects are at the bottom of the steps, define the total gravitational potential energy of the three-object system to be zero. Each answer requires the numerical coefficient to an algebraic expression that uses some combination of the variables , and , where is the acceleration due to gravity. Enter only the numerical coefficient. (Example: If the answer is , just enter 1.23 ) If the objects are positioned on the steps as shown, what is gravitational potential energy of the system? If you redefine the reference height such that the total potential energy of the system is zero, how high above the bottom of the stairs is the new reference height? Now, find a new reference height (measured from the base of the stairs) such that the highest two objects have the exact same gravitational potential energy.
Expert Answer
The potential energy of the system is,