(Solved): The table below gives the list price and the number of bids received for five randomly selected ite ...

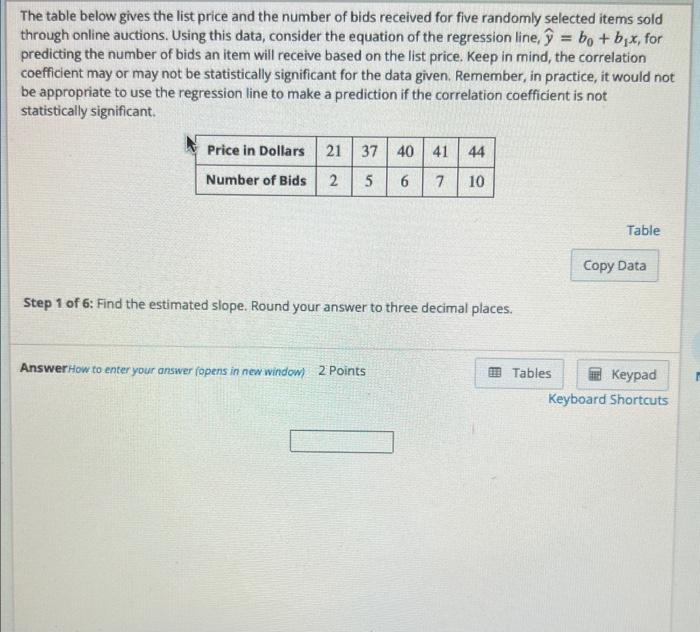
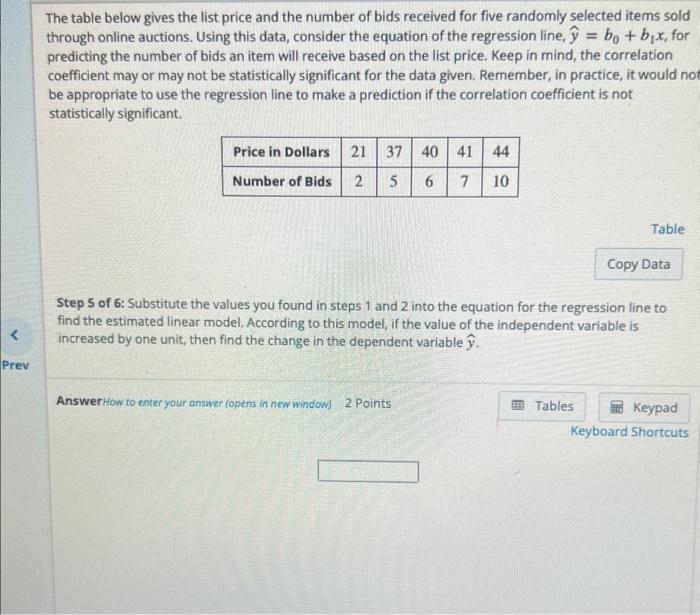
The table below gives the list price and the number of bids received for five randomly selected items sold through online auctions. Using this data, consider the equation of the regression line, \( \hat{y}=b_{0}+b_{1} x \), for predicting the number of bids an item will receive based on the list price. Keep in mind, the correlation coefficient may or may not be statistically significant for the data given. Remember, in practice, it would not be appropriate to use the regression line to make a prediction if the correlation coefficient is not statistically significant. Table Step 1 of 6: Find the estimated slope. Round your answer to three decimal places. Answer How to enter your answer fopens in newwindow). 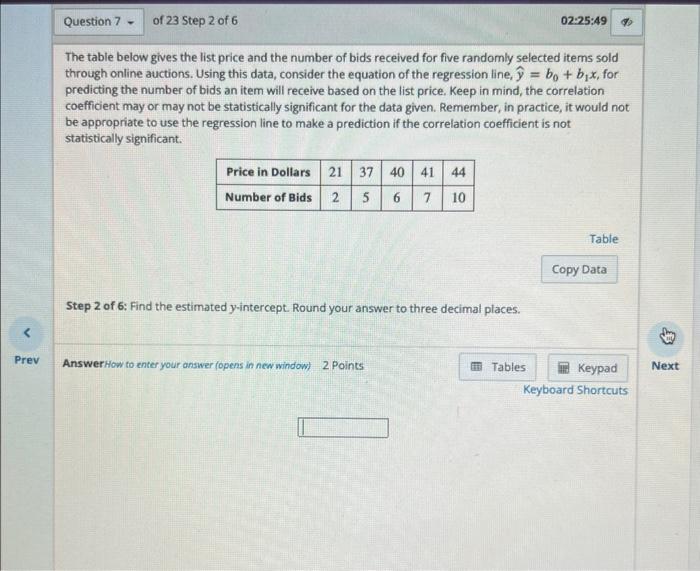2 Points The table below gives the list price and the number of bids received for five randomly selected items sold through online auctions. Using this data, consider the equation of the regression line, \( \hat{y}=b_{0}+b_{1} x \), for predicting the number of bids an item will receive based on the list price. Keep in mind, the correlation coefficient may or may not be statistically significant for the data given. Remember, in practice, it would not be appropriate to use the regression line to make a prediction if the correlation coefficient is not statistically significant. Step 2 of \( 6: \) Find the estimated \( y \)-intercept. Round your answer to three decimal places. 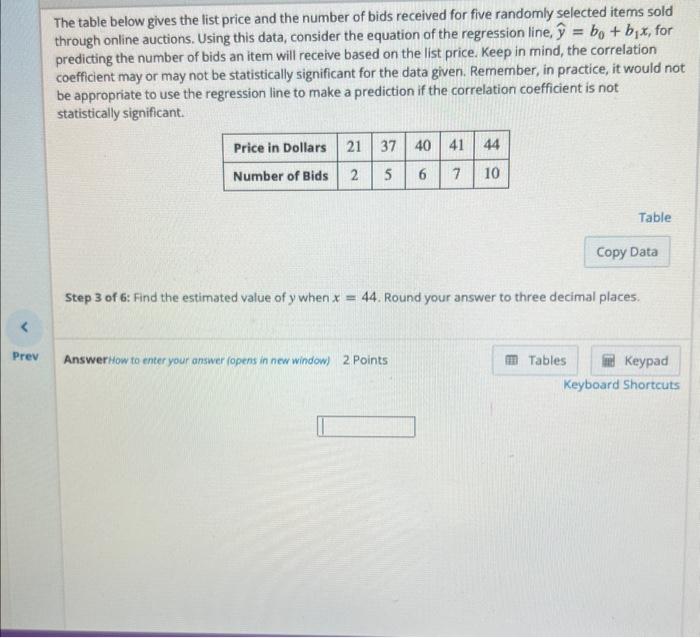Table Answer How to enter your answer (opens in new window) 2 Points The table below gives the list price and the number of bids received for five randomly selected items sold through online auctions. Using this data, consider the equation of the regression line, \( \hat{y}=b_{0}+b_{1} x \), for predicting the number of bids an item will receive based on the list price. Keep in mind, the correlation coefficient may or may not be statistically significant for the data given. Remember, in practice, it would not be appropriate to use the regression line to make a prediction if the correlation coefficient is not statistically significant. Table Step 3 of 6: Find the estimated value of \( y \) when \( x=44 \). Round your answer to three decimal places. 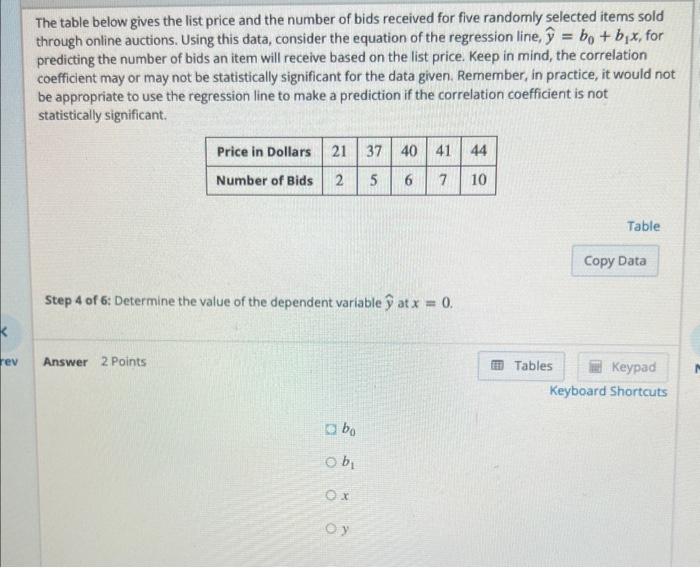The table below gives the list price and the number of bids received for five randomly selected items sold through online auctions. Using this data, consider the equation of the regression line, \( \hat{y}=b_{0}+b_{1} x \), for predicting the number of bids an item will receive based on the list price. Keep in mind, the correlation coefficient may or may not be statistically significant for the data given. Remember, in practice, it would not be appropriate to use the regression line to make a prediction if the correlation coefficient is not statistically significant. Table Step 4 of 6: Determine the value of the dependent variable \( \hat{y} \) at \( x=0 \). Answer 2 Points Keyboard Shortcuts \( b_{0} \) \( b_{1} \) \( x \) \( y \) The table below gives the list price and the number of bids received for five randomly selected items sold through online auctions. Using this data, consider the equation of the regression line, \( \hat{y}=b_{0}+b_{1} x \), for predicting the number of bids an item will receive based on the list price. Keep in mind, the correlation coefficient may or may not be statistically significant for the data given. Remember, in practice, it would no be appropriate to use the regression line to make a prediction if the correlation coefficient is not statistically significant. Table Step 5 of 6: Substitute the values you found in steps 1 and 2 into the equation for the regression line to find the estimated linear model. According to this model, if the value of the independent variable is increased by one unit, then find the change in the dependent variable \( \hat{y} \). 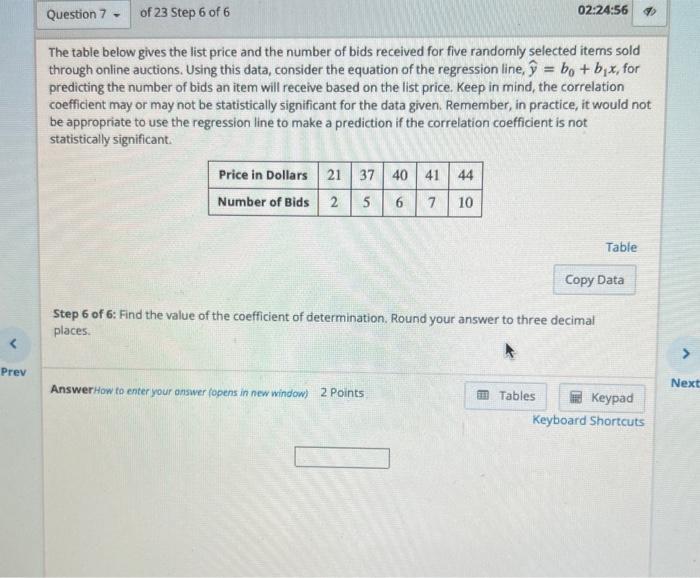The table below gives the list price and the number of bids received for five randomly selected items sold through online auctions. Using this data, consider the equation of the regression line, \( \hat{y}=b_{0}+b_{1} x \), for predicting the number of bids an item will receive based on the list price. Keep in mind, the correlation coefficient may or may not be statistically significant for the data given. Remember, in practice, it would not. be appropriate to use the regression line to make a prediction if the correlation coefficient is not statistically significant. Table Step 6 of 6: Find the value of the coefficient of determination. Round your answer to three decimal places.