Home /
Expert Answers /
Mechanical Engineering /
the-slider-crank-mechanism-is-given-in-the-vertical-plane-as-shown-below-the-load-f-t-is-applied-pa908
(Solved): The slider crank mechanism is given in the vertical plane as shown below. The load F(t) is applied ...
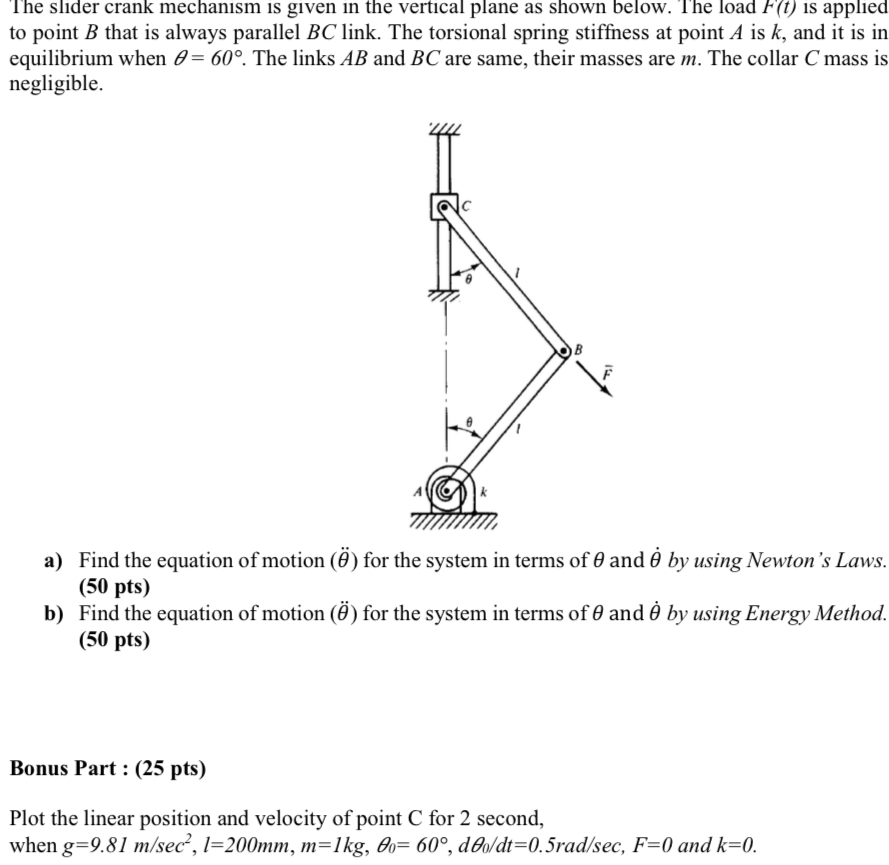
The slider crank mechanism is given in the vertical plane as shown below. The load
F(t)is applied to point
Bthat is always parallel
BClink. The torsional spring stiffness at point
Ais
k, and it is in equilibrium when
\theta =60\deg . The links
ABand
BCare same, their masses are
m. The collar
Cmass is negligible. a) Find the equation of motion
(\theta ^(¨))for the system in terms of
\theta and
\theta ^(?)by using Newton's Laws. pts) b) Find the equation of motion
(\theta ^(¨))for the system in terms of
\theta and
\theta ^(?)by using Energy Method. pts) Bonus Part : (25 pts) Plot the linear position and velocity of point
Cfor 2 second, when
g=9.81(m)/(sec^(2),l)=200mm,m=1kg,\theta _(0)=60\deg ,d(\theta _(0))/(d)t=0.5ra(d)/(sec,F)=0and
k=0.