(Solved): The recurrence relation for merge sort is: \[ \begin{array}{l} T(n)=T(n / 2)+O(1) \\ T(n)=2 T(n / ...

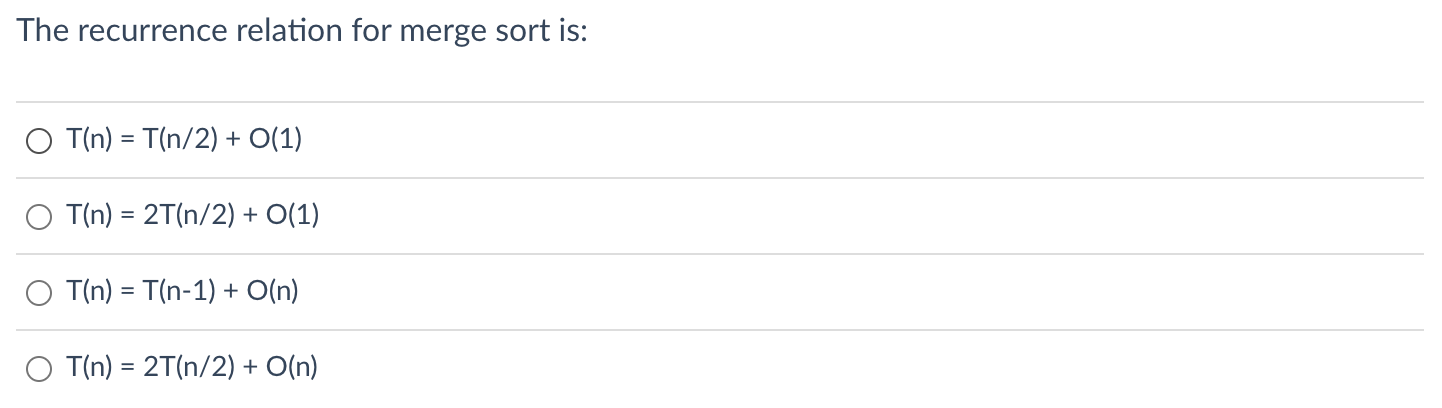
The recurrence relation for merge sort is: \[ \begin{array}{l} T(n)=T(n / 2)+O(1) \\ T(n)=2 T(n / 2)+O(1) \\ T(n)=T(n-1)+O(n) \\ T(n)=2 T(n / 2)+O(n) \end{array} \] Consider this recurrence relation: \[ \begin{aligned} T(1) &=1 \\ T(2) &=1 \\ T(n) &=4 T(n-2)+2 n^{2} \text { for } n>2 \end{aligned} \] The Master Theorem tells us \[ \begin{array}{l} T(n) \epsilon \Theta\left(n^{3}\right) \\ T(n) \epsilon \Theta\left(n^{2} \log n\right) \\ T(n) \epsilon \Theta\left(n^{2}\right) \\ T(n) \epsilon \Theta(n \log n) \end{array} \] nothing