(Solved): The recently popular game Wordle challenges you to guess a five-letter secret ...

???????

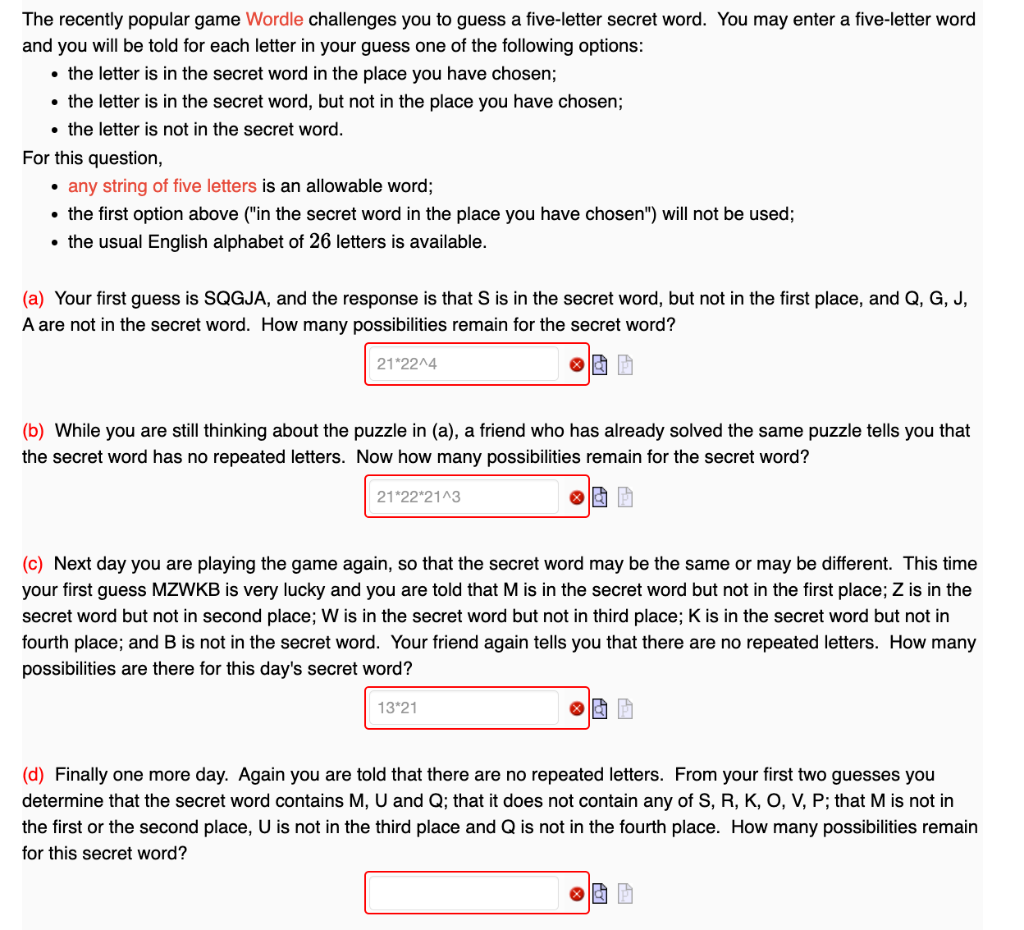
The recently popular game Wordle challenges you to guess a five-letter secret word. You may enter a five-letter word and you will be told for each letter in your guess one of the following options: - the letter is in the secret word in the place you have chosen; - the letter is in the secret word, but not in the place you have chosen; - the letter is not in the secret word. For this question, - any string of five letters is an allowable word; - the first option above ("in the secret word in the place you have chosen") will not be used; - the usual English alphabet of 26 letters is available. (a) Your first guess is SQGJA, and the response is that \( S \) is in the secret word, but not in the first place, and Q, G, J, \( A \) are not in the secret word. How many possibilities remain for the secret word? (b) While you are still thinking about the puzzle in (a), a friend who has already solved the same puzzle tells you that the secret word has no repeated letters. Now how many possibilities remain for the secret word? (c) Next day you are playing the game again, so that the secret word may be the same or may be different. This time your first guess MZWKB is very lucky and you are told that \( M \) is in the secret word but not in the first place; \( Z \) is in the secret word but not in second place; \( \mathrm{W} \) is in the secret word but not in third place; \( \mathrm{K} \) is in the secret word but not in fourth place; and B is not in the secret word. Your friend again tells you that there are no repeated letters. How many possibilities are there for this day's secret word? (d) Finally one more day. Again you are told that there are no repeated letters. From your first two guesses you determine that the secret word contains \( M, U \) and \( Q \); that it does not contain any of \( S, R, K, O, V, P ; \) that \( M \) is not in the first or the second place, \( U \) is not in the third place and \( Q \) is not in the fourth place. How many possibilities remain for this secret word?