(Solved): The quadratic regression equation shown below is for a sample of \( n=22 \). Complete parts a throu ...

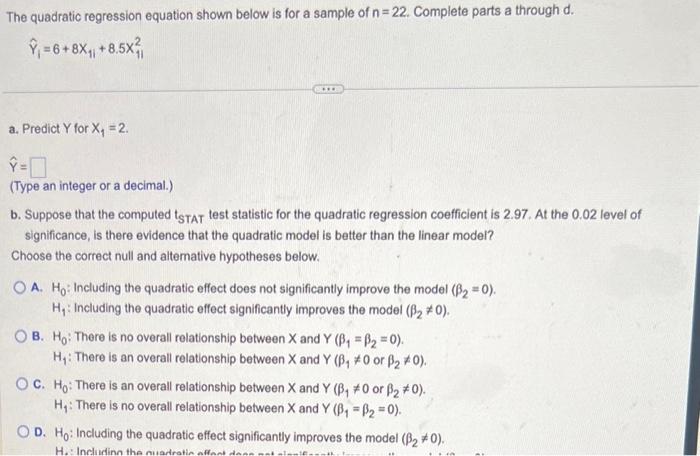
The quadratic regression equation shown below is for a sample of \( n=22 \). Complete parts a through \( d \). \[ \hat{Y}_{1}=6+8 x_{11}+8.5 x_{11}^{2} \] a. Predict \( Y \) for \( X_{1}=2 \). \[ \hat{\mathrm{Y}}= \] (Type an integer or a decimal.) significance, is there evidence that the quadratic model is better than the linear model? Choose the correct null and alternative hypotheses below. A. \( \mathrm{H}_{0} \) : Including the quadratic effect does not significantly improve the model \( \left(\beta_{2}=0\right) \). \( \mathrm{H}_{1} \) : Including the quadratic effect significantly improves the model \( \left(\beta_{2} \neq 0\right) \). B. \( H_{0} \) : There is no overall relationship between \( X \) and \( Y\left(\beta_{1}=\beta_{2}=0\right) \). \( H_{1} \) : There is an overall relationship between \( X \) and \( Y\left(\beta_{1} \neq 0\right. \) or \( \left.\beta_{2} \neq 0\right) \). c. \( H_{0} \) : There is an overall relationship between \( X \) and \( Y\left(\beta_{1} \neq 0\right. \) or \( \left.\beta_{2} \neq 0\right) \). \( H_{1} \) : There is no overall relationship between \( X \) and \( Y\left(\beta_{1}=\beta_{2}=0\right) \). D. \( \mathrm{H}_{0} \) : Including the quadratic effect significantly improves the model \( \left(\beta_{2} \neq 0\right) \). 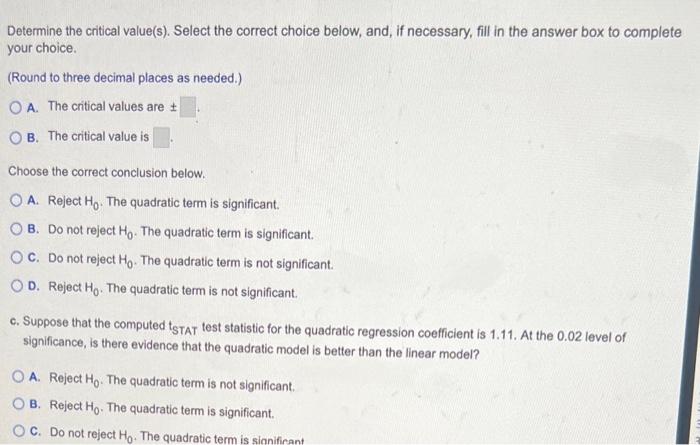Determine the critical value(s). Select the correct choice below, and, if necessary, fill in the answer box to complete your choice. (Round to three decimal places as needed.) A. The critical values are \( \pm \) B. The critical value is Choose the correct conclusion below. A. Reject \( \mathrm{H}_{0} \). The quadratic term is significant. B. Do not reject \( \mathrm{H}_{0} \). The quadratic term is significant. c. Do not reject \( \mathrm{H}_{0} \). The quadratic term is not significant. D. Reject \( \mathrm{H}_{0} \). The quadratic term is not significant. c. Suppose that the computed tsTAT test statistic for the quadratic regression coefficient is 1.11. At the \( 0.02 \) level of significance, is there evidence that the quadratic model is better than the linear model? A. Reject \( \mathrm{H}_{0} \). The quadratic term is not significant. B. Reject \( \mathrm{H}_{0} \). The quadratic term is significant. c. Do not reject \( \mathrm{H}_{0} \). The quadratic term is sionificant d. Suppose the regression coefficient for the linear effect is \( -8.0 \). Predict \( Y \) for \( X_{1}=2 \). \[ \hat{\mathrm{Y}}= \] (Type an integer or a decimal.)