(Solved): The principle of superposition states that if two functions each separately satisfy the wave equati ...

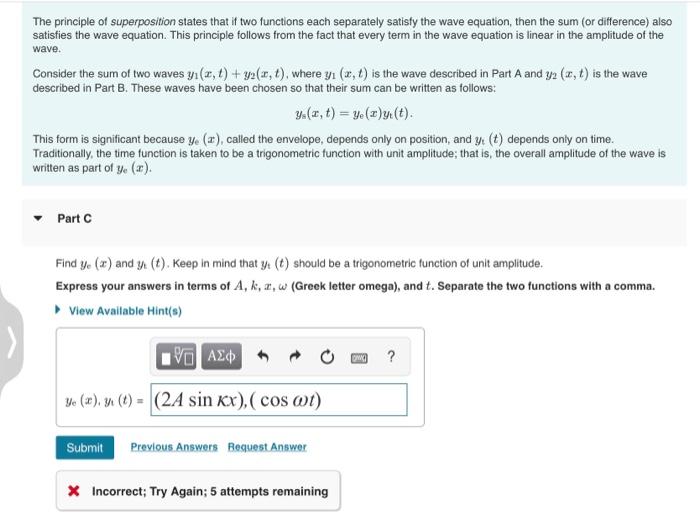
The principle of superposition states that if two functions each separately satisfy the wave equation, then the sum (or difference) also satisfies the wave equation. This principle follows from the fact that every term in the wave equation is linear in the amplitude of the wave. Consider the sum of two waves \( y_{1}(x, t)+y_{2}(x, t) \), where \( y_{1}(x, t) \) is the wave described in Part A and \( y_{2}(x, t) \) is the wave described in Part B. These waves have been chosen so that their sum can be written as follows: \[ y_{s}(x, t)=y_{e}(x) y_{t}(t) \] This form is significant because \( y_{e}(x) \), called the envelope, depends only on position, and \( y_{t}(t) \) depends only on time. Traditionally, the time function is taken to be a trigonometric function with unit amplitude; that is, the overall amplitude of the wave is written as part of \( y_{e}(x) \). Part C Find \( y_{e}(x) \) and \( y_{t}(t) \). Keep in mind that \( y_{t}(t) \) should be a trigonometric function of unit amplitude. Express your answers in terms of \( A, k, x, \omega \) (Greek letter omega), and \( t \). Separate the two functions with a comma. 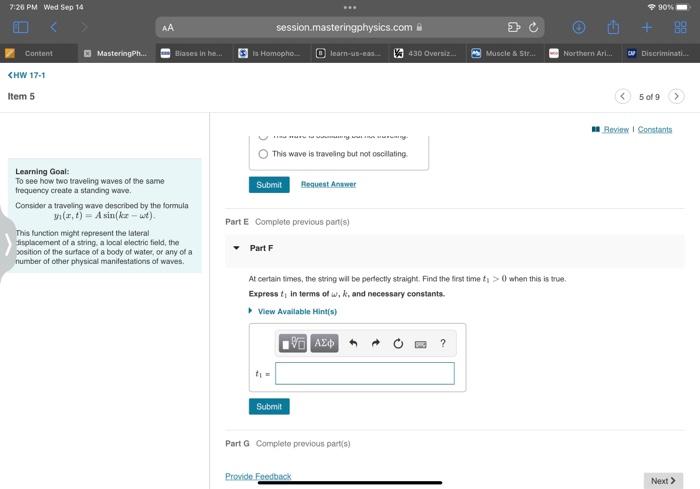2 Incorrect; Try Again; 5 attempts remaining Learning Goal: To see how two traveling waves of the same frequency create a standing wave. Consider a traveling wave described by the formula \[ y_{1}(x, t)=A \sin (k x-\omega t) \text {. } \] Part E Complete previous partis) This function might represent the tateral firplacemeet of a string a bocal electric field, the -osition of the surface of a body of water, or any of a Part F number of ceter physical manifeatations of waves. At certain tmes, the string will be pertectly straight. Find the frst time \( t_{1}>0 \) when this is true: Express \( t_{1} \) in terms of \( w_{1} k \), and necessary constants.