Home /
Expert Answers /
Advanced Math /
the-phase-portraits-correspond-to-linear-systems-of-the-form-x-39-ax-in-which-the-matrix-a-has-two-l-pa536
(Solved): The phase portraits correspond to linear systems of the form X' = Ax in which the matrix A has two l ...
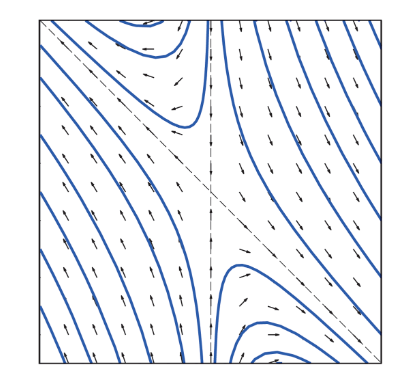
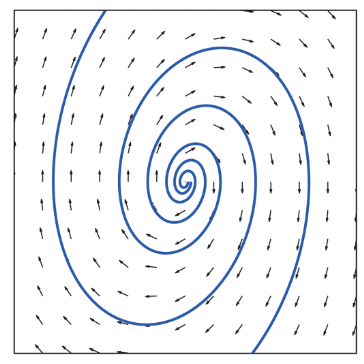
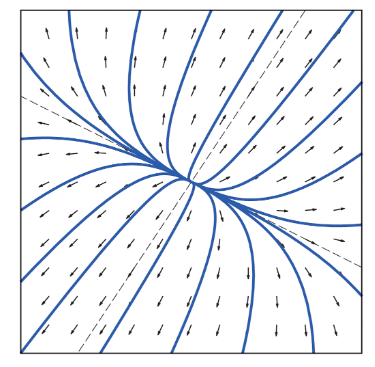
The phase portraits correspond to linear systems of the form X' = Ax in which the matrix A has two linearly independent eigenvectors. Determine the nature of the eigenvalues and eigenvectors of each system. For example, you may discern that the system has pure imaginary eigenvalues, or that it has real eigenvalues of opposite sign; that an eigenvector associated with the positive eigenvalue is roughly ...
1:
2:
3: