(Solved): The mean yearly rainfall in Sydney, Australia, is about \( 137 \mathrm{~mm} \) and the standard dev ...

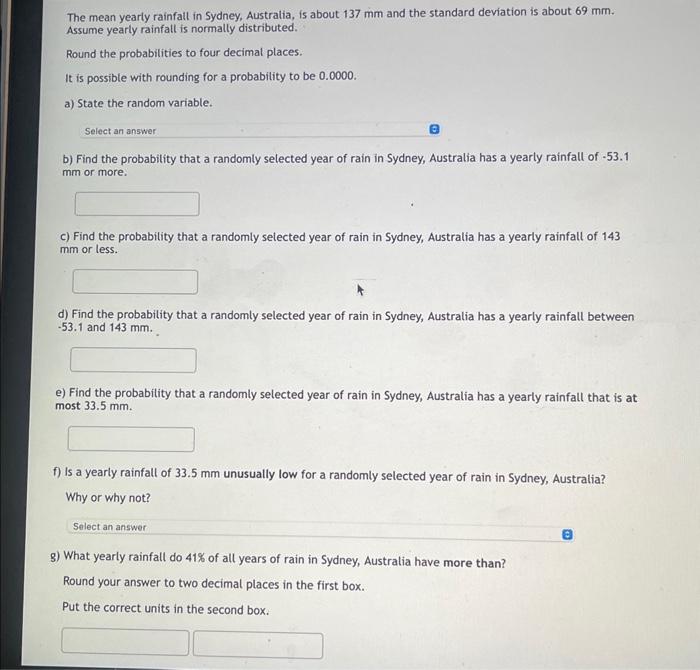
The mean yearly rainfall in Sydney, Australia, is about \( 137 \mathrm{~mm} \) and the standard deviation is about \( 69 \mathrm{~mm} \). Assume yearly rainfall is normally distributed. Round the probabilities to four decimal places. It is possible with rounding for a probability to be \( 0.0000 \). a) State the random variable. b) Find the probability that a randomly selected year of rain in Sydney, Australia has a yearly rainfall of \( -53.1 \) \( \mathrm{mm} \) or more. c) Find the probability that a randomly selected year of rain in Sydney, Australia has a yearly rainfall of 143 \( \mathrm{mm} \) or less. d) Find the probability that a randomly selected year of rain in Sydney, Australia has a yearly rainfall between \( .53 .1 \) and \( 143 \mathrm{~mm} \). e) Find the probability that a randomly selected year of rain in Sydney, Australia has a yearly rainfall that is at most \( 33.5 \mathrm{~mm} \). f) Is a yearly rainfall of \( 33.5 \mathrm{~mm} \) unusually low for a randomly selected year of rain in Sydney, Australia? Why or why not? g) What yearly rainfall do \( 41 \% \) of all years of rain in Sydney, Australia have more than? Round your answer to two decimal places in the first box. Put the correct units in the second box.