(Solved): The Maclaurin series expansion for \( \cos \mathrm{X} \) is: \[ \cos (x)=1-\frac{x^{2}}{2 !}+\frac ...

The Maclaurin series expansion for \( \cos \mathrm{X} \) is: \[ \cos (x)=1-\frac{x^{2}}{2 !}+\frac{x^{4}}{4 !}-\frac{x^{6}}{6 !}+\frac{x^{8}}{8 !} \cdots \] Develop a well-structured MATLAB function to compute the Maclaurin series expansion for cosine. Test your program for \( \theta=\pi / 3\left(60^{\circ}\right) \) and \( \theta=7 \pi / 3\left(420^{\circ}\right) \) Observe the difference in the number of iterations required to obtain the correct result with the desired error criterion of two significant figures. function \( [ \) fx, ea,iter] \( = \) Estcosine(x,sd) \( \% \) Maclaurin series of cosine \( \%[f x \), ea,iter] = Estcosine(x,sd, maxit) \( \% \) input: \( \% x= \) value at which series evaluated \( \% \) sd \( = \) stopping criterion (# of significant digits) \( \% \) \( \% \) output: \( \% \) fx \( = \) estimated value \( \% \) iter \( = \) number of iterations of series \( \% \) initialization iter \( =0 ; \) ea \( =100 ; \) sol \( =0 ; \) es let \( \% \) iterative calculation - while loop while (1) sol \( =0 ; \% \) let this variable be your iterative estimate solution 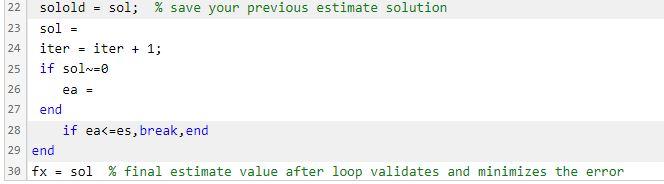22 solold = sol; \% save your previous estimate solution 23 sol \( = \) 24 iter \( = \) iter \( +1 ; \) 25 if sol \( =0 \) 26 ea \( = \) 27 end 28 if eas=es, break,end 29 end \( \mathrm{fx}=\mathrm{sol} \% \) final estimate value after loop validates and minimizes the error 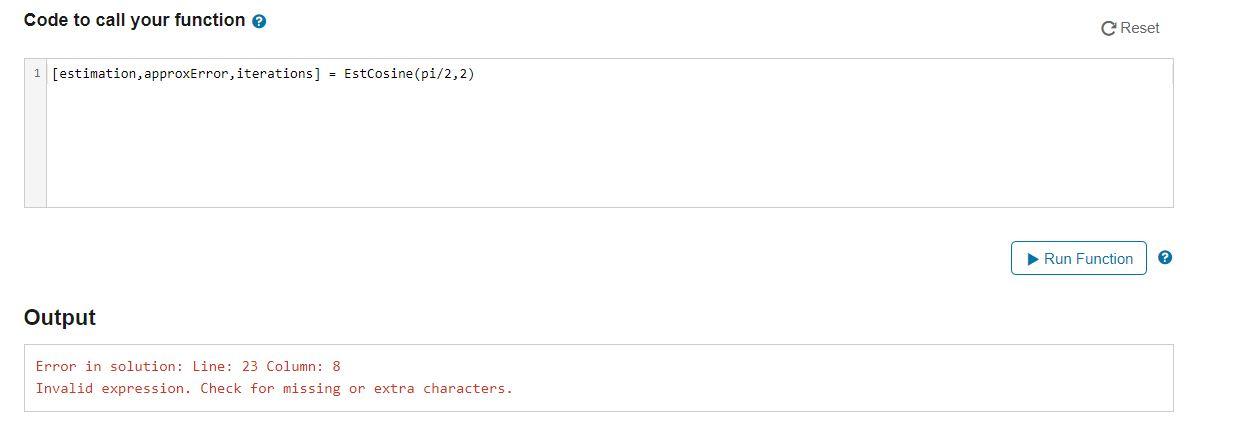Error in solution: Line: 23 Column: 8 Invalid expression. Check for missing or extra characters.