(Solved): The linear transformation \( T: \mathbb{R}^{3} \rightarrow \mathbb{R}^{5} \) below is nilpotent of ...

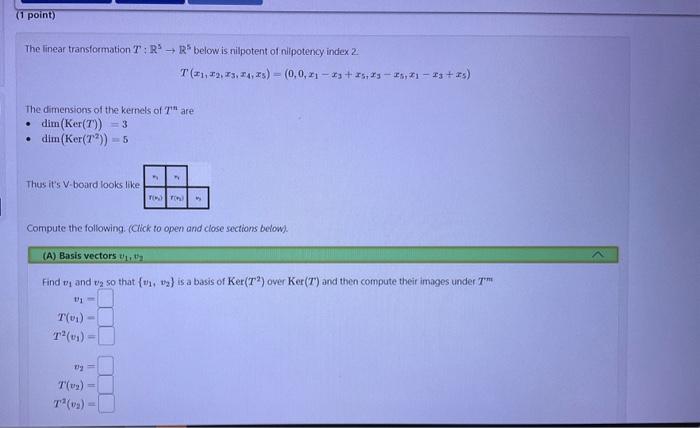
The linear transformation \( T: \mathbb{R}^{3} \rightarrow \mathbb{R}^{5} \) below is nilpotent of nilpotency index 2 . \[ T\left(x_{1}, x_{2}, x_{3}, x_{4}, x_{5}\right)=\left(0,0, x_{1}-x_{3}+x_{5}, x_{3}-x_{5}, x_{1}-x_{3}+x_{5}\right) \] The dimensions of the kemets of \( T^{\text {in }} \) are - \( \operatorname{dim}(\operatorname{Ker}(T))=3 \) - \( \operatorname{dim}\left(\operatorname{Ker}\left(T^{2}\right)\right)=5 \) Thus it's V-board looks like Compute the following. (Click to open and close sections betow). 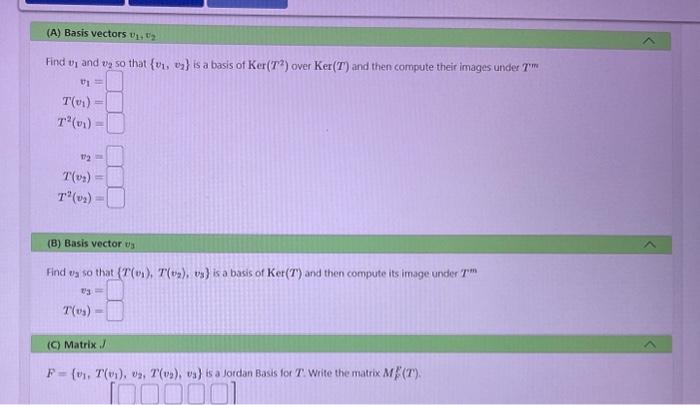(A) Basis vectors \( v_{1}, t_{2} \) Find \( v_{1} \) and \( v_{2} \) so that \( \left\{v_{1}, v_{2}\right\} \) is a basis of \( \operatorname{Ker}\left(T^{2}\right) \) over Ker \( (T) \) and then compute their images under \( T^{m} \) \[ \begin{array}{r} v_{1}= \\ T\left(v_{1}\right)= \\ T^{2}\left(v_{1}\right)= \\ v_{2}= \\ T\left(v_{2}\right)= \\ T^{2}\left(v_{2}\right)= \end{array} \] Find \( v_{1} \) and \( v_{2} \) so that \( \left\{v_{1}, v_{2}\right\} \) is a basis of \( \operatorname{Ker}\left(T^{2}\right) \) over \( \operatorname{Ker}(T) \) and then compute their images under \( T^{m} \) \[ \begin{aligned} v_{1} & = \\ T\left(v_{1}\right) & = \\ T^{2}\left(v_{1}\right) & = \\ v_{2} & = \\ T\left(v_{2}\right) & = \\ T^{2}\left(v_{2}\right) & = \end{aligned} \] (B) Basis vector \( v_{3} \) Find \( v_{2} \) so that \( \left\{T\left(v_{1}\right), T\left(v_{2}\right), v_{3}\right\} \) is a basis of \( \operatorname{Ker}(T) \) and then compute its image under \( T^{m} \) \[ \begin{array}{r} v_{3}= \\ T\left(v_{3}\right)= \end{array} \] (C) Matrix J \( F=\left\{v_{1}, T\left(v_{1}\right), v_{2}, T\left(v_{2}\right), v_{3}\right\} \) is a Jordan Basis for \( T \). Write the matrix \( M_{F}^{F}(T) \). \[ \begin{array}{r} v_{3}= \\ T\left(v_{3}\right)= \end{array} \] (C) Matrix J \( F=\left\{v_{1}, T\left(v_{1}\right), v_{2}, T\left(v_{2}\right), v_{3}\right\} \) is a Jordan Basis for \( T \). Write the matrix \( M_{F}^{F}(T) \). Note: You can earn partial credit on this problem. You have attempted this problem 0 times. You have unlimited attempts remaining.