(Solved): The function \( f(x)=\frac{1}{\sqrt{2 \pi}} e^{\frac{-(x-c)^{2}}{2 b^{2}}} \) defines the Gaussian ...

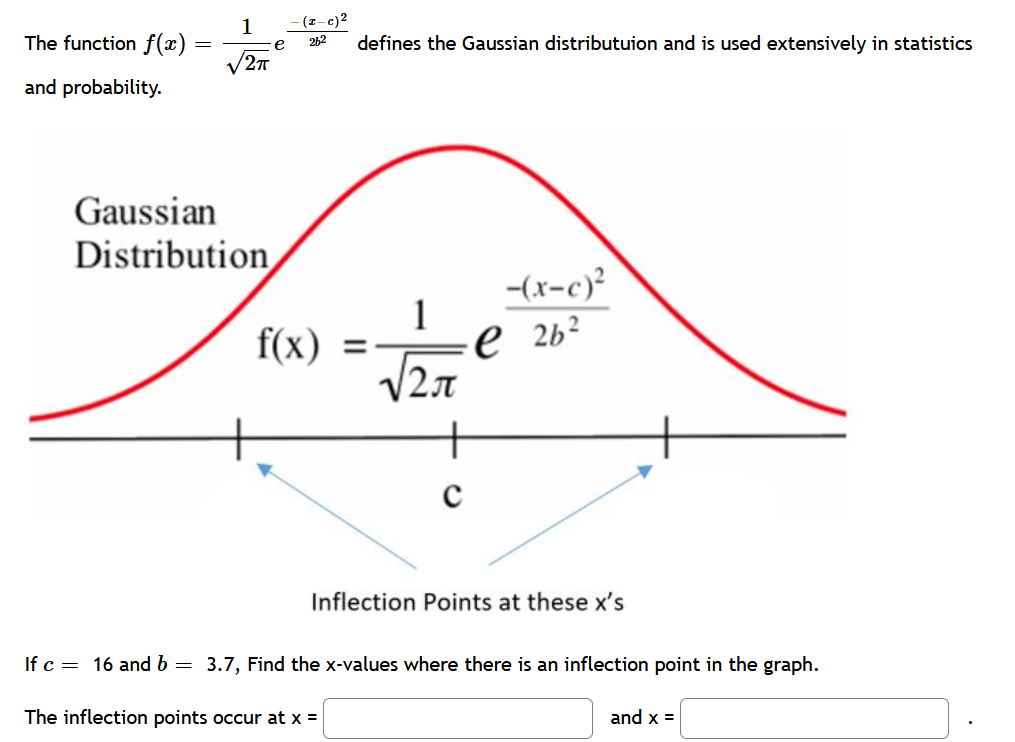
The function \( f(x)=\frac{1}{\sqrt{2 \pi}} e^{\frac{-(x-c)^{2}}{2 b^{2}}} \) defines the Gaussian distributuion and is used extensively in statistics and probability. Inflection Points at these \( x^{\prime} s \) If \( c=16 \) and \( b=3.7 \), Find the \( \mathrm{x} \)-values where there is an inflection point in the graph. The inflection points occur at \( x= \) and \( \mathrm{x}= \)