(Solved): The equation of the least squares regression line is \( \hat{y}=2.0233 x-2.3256 \) and the sum of s ...

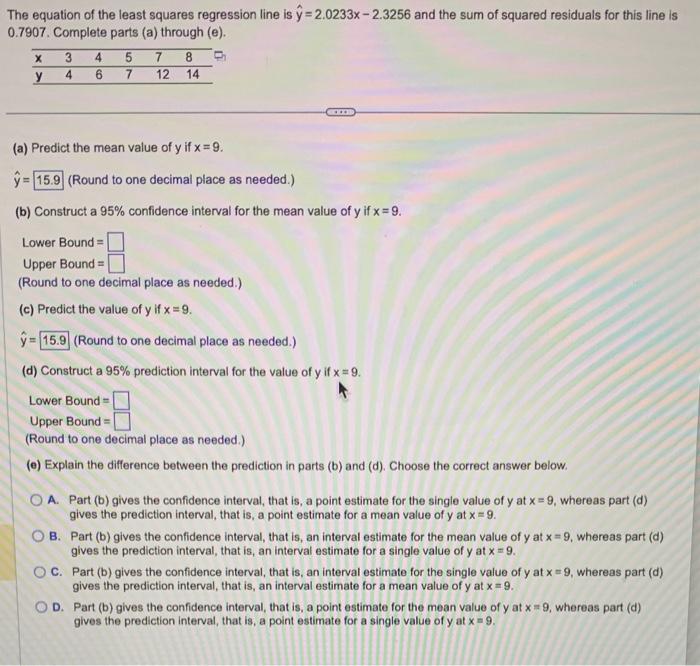
The equation of the least squares regression line is \( \hat{y}=2.0233 x-2.3256 \) and the sum of squared residuals for this line is \( 0.7907 \). Complete parts (a) through \( (e) \). (a) Predict the mean value of \( y \) if \( x=9 \). \( \hat{y}=\quad \) (Round to one decimal place as needed.) (b) Construct a \( 95 \% \) confidence interval for the mean value of \( y \) if \( x=9 \). Lower Bound \( = \) Upper Bound = (Round to one decimal place as needed.) (c) Predict the value of \( y \) if \( x=9 \). \( \hat{y}=\quad \) (Round to one decimal place as needed.) (d) Construct a \( 95 \% \) prediction interval for the value of \( y \) if \( x=9 \). Lower Bound \( = \) Upper Bound = (Round to one decimal place as needed.) (e) Explain the difference between the prediction in parts (b) and (d). Choose the correct answer below. A. Part (b) gives the confidence interval, that is, a point estimate for the single value of \( y \) at \( x=9 \), whereas part (d) gives the prediction interval, that is, a point estimate for a mean value of \( y \) at \( x=9 \). B. Part (b) gives the confidence interval, that is, an interval estimate for the mean value of \( y \) at \( x=9 \), whereas part (d) gives the prediction interval, that is, an interval estimate for a single value of \( y \) at \( x=9 \). C. Part (b) gives the confidence interval, that is, an interval estimate for the single value of \( y \) at \( x=9 \), whereas part (d) gives the prediction interval, that is, an interval estimate for a mean value of \( y \) at \( x=9 \). D. Part (b) gives the confidence interval, that is, a point estimate for the mean value of \( y \) at \( x=9 \), whereas part (d) gives the prediction interval, that is, a point estimate for a single value of \( y \) at \( x=9 \).