(Solved): The equation of motion of a spring-mass-damper system subjected to a harmonic force can be expre ...

The equation of motion of a spring-mass-damper system subjected to a harmonic force can be expressed as \[ \ddot{x}+2 \zeta \omega_{n} \dot{x}+\omega_{n}^{2}=f_{0} \cos \omega t \] where \( f_{0}=\frac{F_{0}}{m}, \omega_{n}=\sqrt{\frac{k}{m}} \), and \( \zeta=c /\left(2 m \omega_{n}\right) \). i. Find the steady-state response of the system in the form \( x_{s}(t)=C_{1} \cos \omega t+C_{2} \sin \omega t \) ii. Find the total response of the system in the form \[ x(t)=x_{h}(t)+x_{p}(t)=A \cos \omega_{d} t+B \sin \omega_{d} t+C_{1} \cos \omega t+C_{2} \sin \omega t \] Assume the initial conditions of the system as \( x(t=0)=x_{0} \) and \( \dot{x}(t=0)=\dot{x}_{0} \). 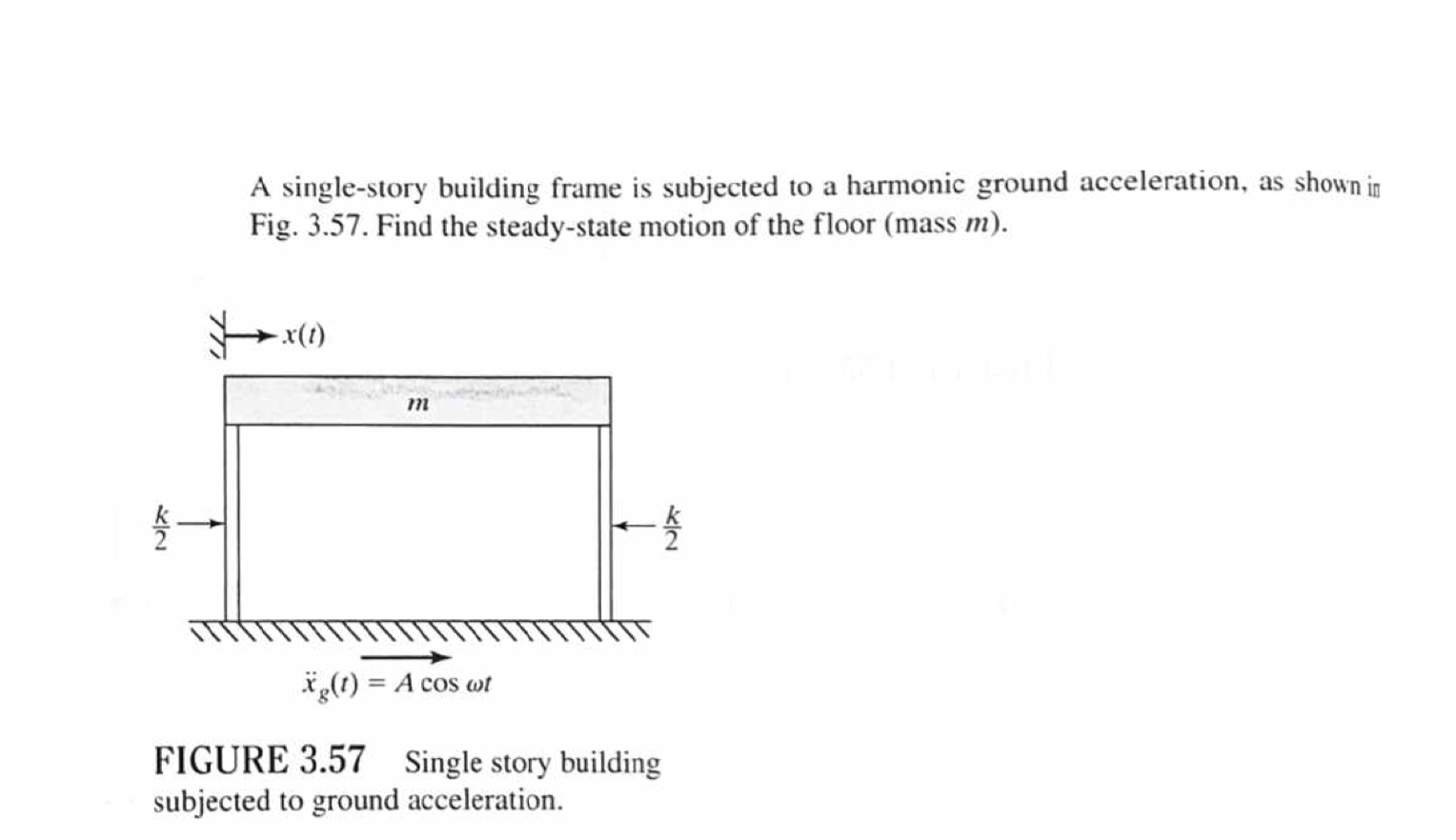A single-story building frame is subjected to a harmonic ground acceleration, as shown in Fig. 3.57. Find the steady-state motion of the floor (mass \( m \) ). FIGURE 3.57 Single story building subjected to ground acceleration.