(Solved): The energy stored in the circuit shown is zero at the time when the switch is closed. a. Find the ...

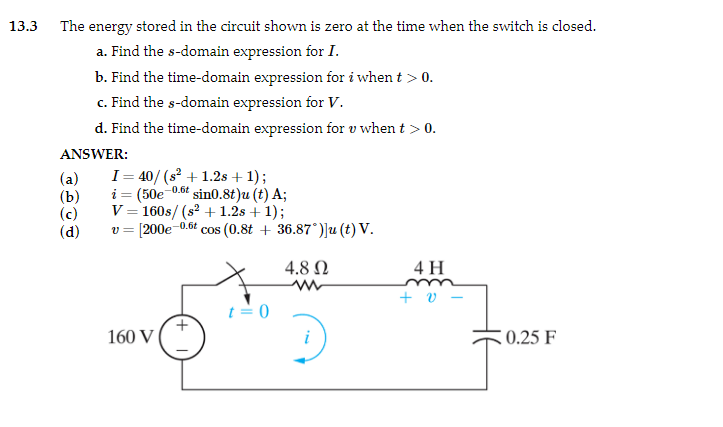
The energy stored in the circuit shown is zero at the time when the switch is closed. a. Find the \( s \)-domain expression for \( I \). b. Find the time-domain expression for \( i \) when \( t>0 \). c. Find the \( s \)-domain expression for \( V \). d. Find the time-domain expression for \( v \) when \( t>0 \). 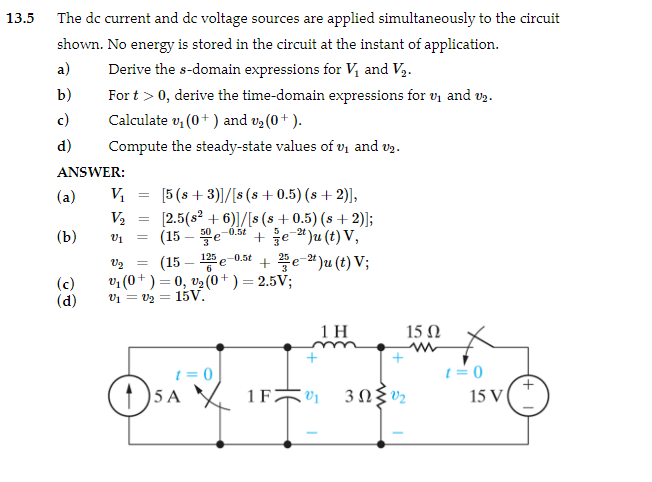ANSWER: (a) \( I=40 /\left(s^{2}+1.2 s+1\right) \); (b) \( \quad i=\left(50 e^{-0.6 t} \sin 0.8 t\right) u(t) \mathrm{A} \); (c) \( \quad V=160 s /\left(s^{2}+1.2 s+1\right) \) (d) \( \quad v=\left[200 e^{-0.6 t} \cos \left(0.8 t+36.87^{\circ}\right)\right] u(t) \mathrm{V} \) 5 The dc current and dc voltage sources are applied simultaneously to the circuit shown. No energy is stored in the circuit at the instant of application. a) Derive the \( s \)-domain expressions for \( V_{1} \) and \( V_{2} \). b) For \( t>0 \), derive the time-domain expressions for \( v_{1} \) and \( v_{2} \). c) Calculate \( v_{1}\left(0^{+}\right) \)and \( v_{2}\left(0^{+}\right) \). d) Compute the steady-state values of \( v_{1} \) and \( v_{2} \). ANSWER: (a) \( \quad V_{1}=[5(s+3)] /[s(s+0.5)(s+2)] \), \( V_{2}=\left[2.5\left(s^{2}+6\right)\right] /[s(s+0.5)(s+2)] ; \) (b) \( \quad v_{1}=\left(15-\frac{50}{3} e^{-0.5 t}+\frac{5}{3} e^{-2 t}\right) u(t) \mathrm{V} \), \( v_{2}=\left(15-\frac{125}{6} e^{-0.5 t}+\frac{25}{3} e^{-2 t}\right) u(t) \mathrm{V} \); (c) \( \quad v_{1}\left(0^{+}\right)=0, v_{2}\left(0^{+}\right)=2.5 \mathrm{~V} \); (d) \( \quad v_{1}=v_{2}^{\prime}=15 \mathrm{~V} \).