(Solved): The digit sum of a natural number is the sum of its component digits. For example, the digit sum ...

The digit sum of a natural number is the sum of its component digits. For example, the digit sum of 40 is \( 4+0=4 \), and the digit sum of 86 is \( 8+6=14 \). A 4-digit number is any integer \( n \) such that \( 1000 \leq n \leq 9999 \) Syntax advice: - To enter \( C(n, k) \), type either \( \mathrm{C}(\mathrm{n}, \mathrm{k}) \) or \( \operatorname{comb}(\mathrm{n}, \mathrm{k}) \). - To enter \( P(n, k) \), type either \( \mathrm{P}(\mathrm{n}, \mathrm{k}) \) or \( \operatorname{perm}(\mathrm{n}, \mathrm{k}) \). - To enter \( n^{k} \), type \( \mathbf{n}^{\wedge} \mathbf{k} \). - A/ways use * for multiplication. For example, \( 2 x \) should be entered as \( 2{ }^{\star} \mathbf{x} \). (a) How many 4-digit numbers have a digit sum divisible by 3 ? Q (b) How many 4-digit numbers have a digit sum equal to 35 ? Q 0 (c) How many 4-digit numbers have a digit sum equal to 21? ? 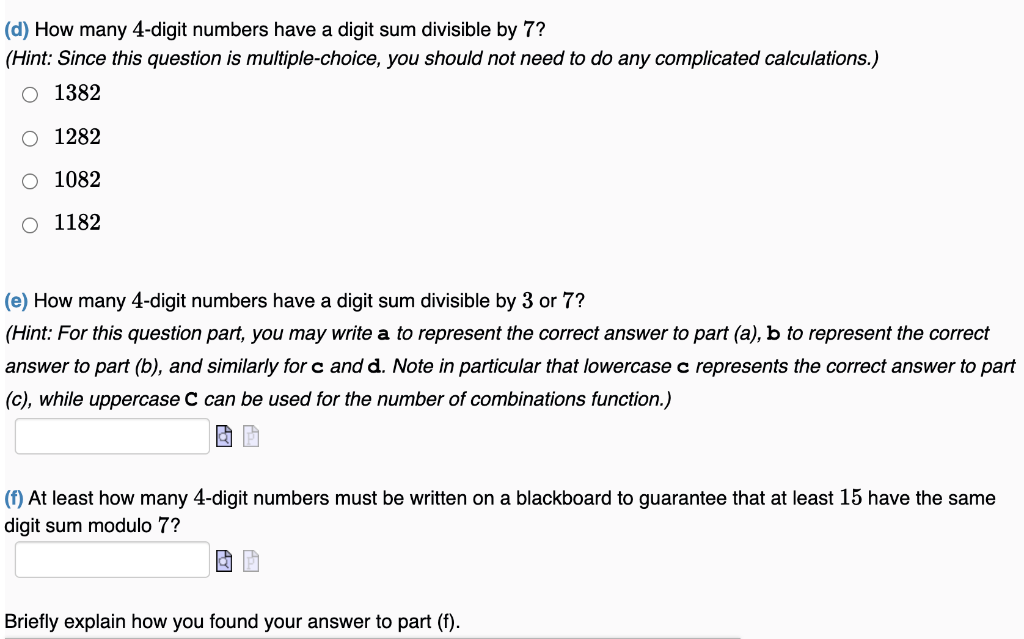(d) How many 4-digit numbers have a digit sum divisible by 7 ? (Hint: Since this question is multiple-choice, you should not need to do any complicated calculations.) 1382 158 1082 1182 (e) How many 4-digit numbers have a digit sum divisible by 3 or 7 ? (Hint: For this question part, you may write a to represent the correct answer to part (a), b to represent the correct answer to part (b), and similarly for \( \mathrm{c} \) and \( \mathrm{d} \). Note in particular that lowercase c represents the correct answer to part (c), while uppercase \( \mathrm{C} \) can be used for the number of combinations function.) ? (f) At least how many 4-digit numbers must be written on a blackboard to guarantee that at least 15 have the same digit sum modulo 7 ? ? Briefly explain how you found your answer to part (f).