(Solved): The diagram shows a pendulum arm, B, of length \( \mathrm{L} \), which is pinned by a revolute join ...

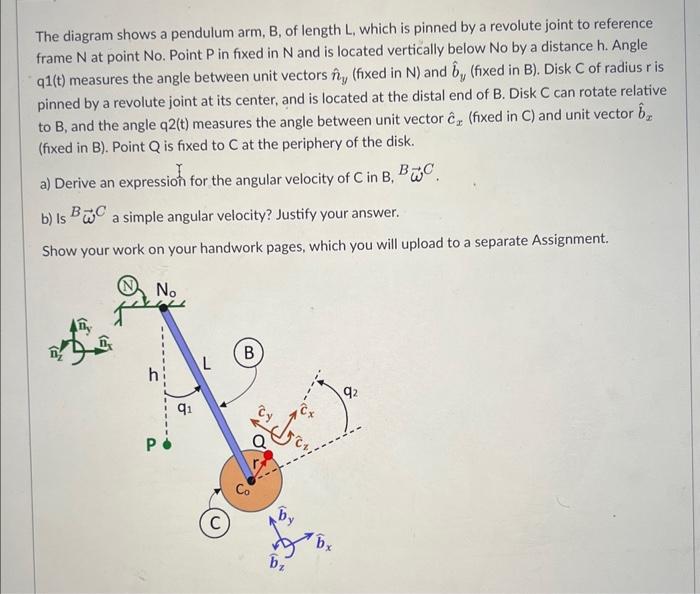
The diagram shows a pendulum arm, B, of length \( \mathrm{L} \), which is pinned by a revolute joint to reference frame \( \mathrm{N} \) at point No. Point \( \mathrm{P} \) in fixed in \( \mathrm{N} \) and is located vertically below No by a distance \( \mathrm{h} \). Angle \( \mathrm{q} 1(\mathrm{t}) \) measures the angle between unit vectors \( \hat{n}_{y} \) (fixed in \( \mathrm{N} \) ) and \( \hat{b}_{y} \) (fixed in B). Disk \( \mathrm{C} \) of radius \( r \) is pinned by a revolute joint at its center, and is located at the distal end of B. Disk \( C \) can rotate relative to \( \mathrm{B} \), and the angle \( \mathrm{q} 2\left(\mathrm{t}\right. \) ) measures the angle between unit vector \( \hat{c}_{x} \) (fixed in \( \mathrm{C} \) ) and unit vector \( \hat{b}_{x} \) (fixed in \( B \) ). Point \( Q \) is fixed to \( C \) at the periphery of the disk. a) Derive an expression for the angular velocity of \( C \) in \( B, B \vec{\omega} C \). b) Is \( B \vec{\omega}^{C} \) a simple angular velocity? Justify your answer. Show your work on your handwork pages, which you will upload to a separate Assignment.