(Solved): The average student-loan debt is reported to be \( \$ 25,235 \) with a population standard deviatio ...

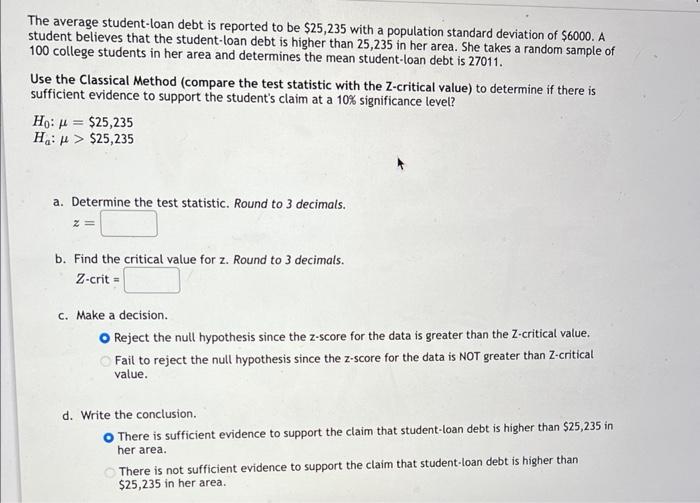
The average student-loan debt is reported to be \( \$ 25,235 \) with a population standard deviation of \( \$ 6000 \). A student believes that the student-loan debt is higher than 25,235 in her area. She takes a random sample of 100 college students in her area and determines the mean student-loan debt is 27011. Use the Classical Method (compare the test statistic with the Z-critical value) to determine if there is sufficient evidence to support the student's claim at a \( 10 \% \) significance level? \[ \begin{array}{l} H_{0}: \mu=\$ 25,235 \\ H_{a}: \mu>\$ 25,235 \end{array} \] a. Determine the test statistic. Round to 3 decimals. \[ z= \] b. Find the critical value for \( z \). Round to 3 decimals. \( Z \)-crit = c. Make a decision. Reject the null hypothesis since the \( \mathrm{z} \)-score for the data is greater than the \( \mathrm{Z} \)-critical value. Fail to reject the null hypothesis since the \( z \)-score for the data is NOT greater than \( z \)-critical value. d. Write the conclusion. There is sufficient evidence to support the claim that student-loan debt is higher than \( \$ 25,235 \) in her area. There is not sufficient evidence to support the claim that student-loan debt is higher than \( \$ 25,235 \) in her area.