(Solved): The average American consumes 94 liters of alcohol per year. Does the average college student cons ...

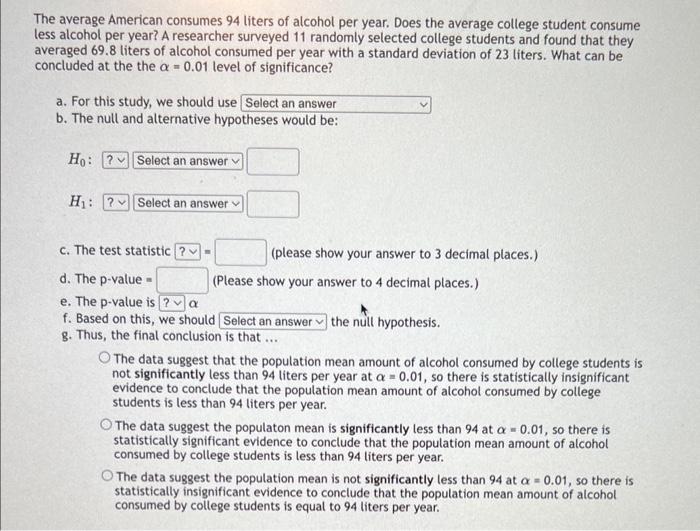
The average American consumes 94 liters of alcohol per year. Does the average college student consume less alcohol per year? A researcher surveyed 11 randomly selected college students and found that they averaged \( 69.8 \) liters of alcohol consumed per year with a standard deviation of 23 liters. What can be concluded at the the \( \alpha=0.01 \) level of significance? a. For this study, we should use b. The null and alternative hypotheses would be: \( H_{0} \) : \( H_{1} \) : c. The test statistic = (please show your answer to 3 decimal places.) d. The \( p \)-value = \( \quad \) (Please show your answer to 4 decimal places.) e. The p-value is \( \alpha \) f. Based on this, we should g. Thus, the final conclusion is that ... the null hypothesis. The data suggest that the population mean amount of alcohol consumed by college students is not significantly less than 94 liters per year at \( \alpha=0.01 \), so there is statistically insignificant evidence to conclude that the population mean amount of alcohol consumed by college students is less than 94 liters per year. The data suggest the populaton mean is significantly less than 94 at \( \alpha=0.01 \), so there is statistically significant evidence to conclude that the population mean amount of alcohol consumed by college students is less than 94 liters per year. The data suggest the population mean is not significantly less than 94 at \( \alpha=0.01 \), so there is statistically insignificant evidence to conclude that the population mean amount of alcohol consumed by college students is equal to 94 liters per year. 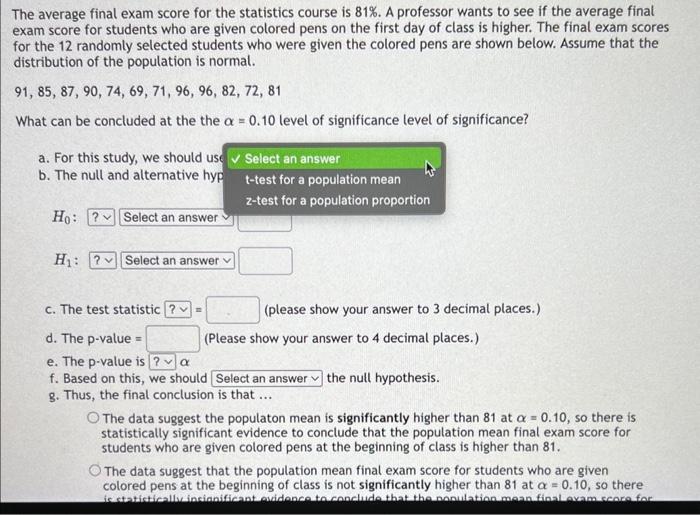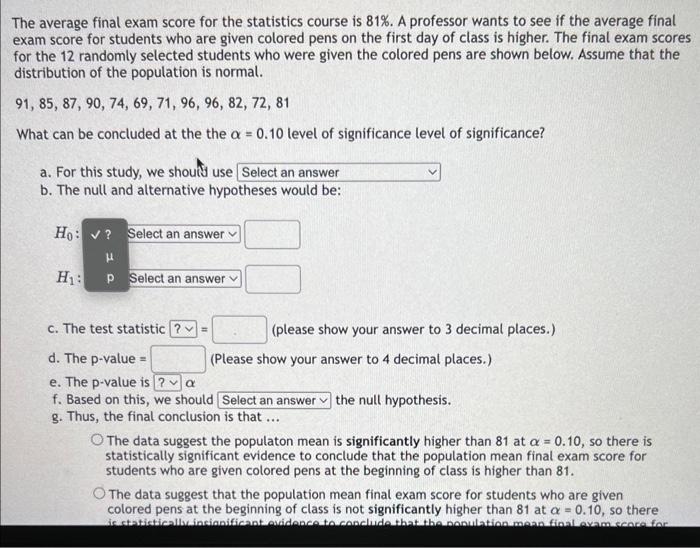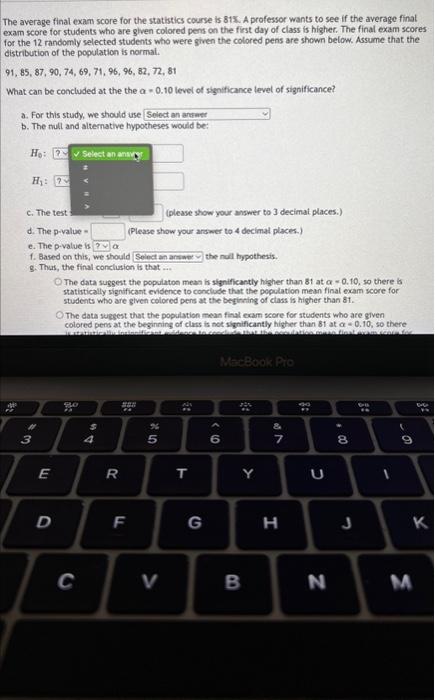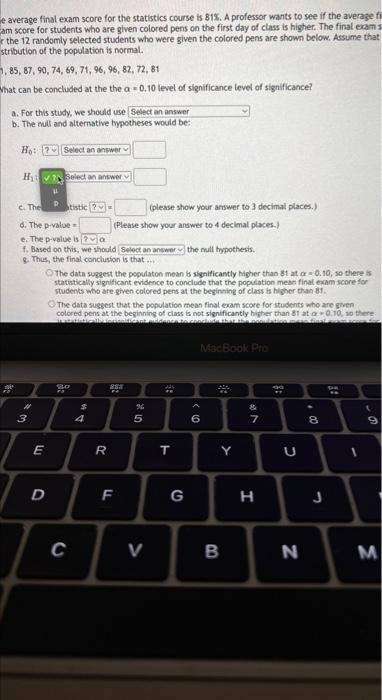The average final exam score for the statistics course is \( 81 \% \). A professor wants to see if the average final exam score for students who are given colored pens on the first day of class is higher. The final exam scores. for the 12 randomly selected students who were given the colored pens are shown below. Assume that the distribution of the population is normal. \( 91,85,87,90,74,69,71,96,96,82,72,81 \) What can be concluded at the the \( \alpha=0.10 \) level of significance level of significance? a. For this study, we should use b. The null and alternative hyp \( H_{0} \) : \( H_{1} \) : c. The test statistic \( =\quad \) (please show your answer to 3 decimal places.) d. The \( p \)-value \( =\quad \) (Please show your answer to 4 decimal places.) e. The p-value is \( \alpha \) f. Based on this, we should the null hypothesis. 8. Thus, the final conclusion is that ... The data suggest the populaton mean is significantly higher than 81 at \( \alpha=0.10 \), so there is statistically significant evidence to conclude that the population mean final exam score for students who are given colored pens at the beginning of class is higher than 81. 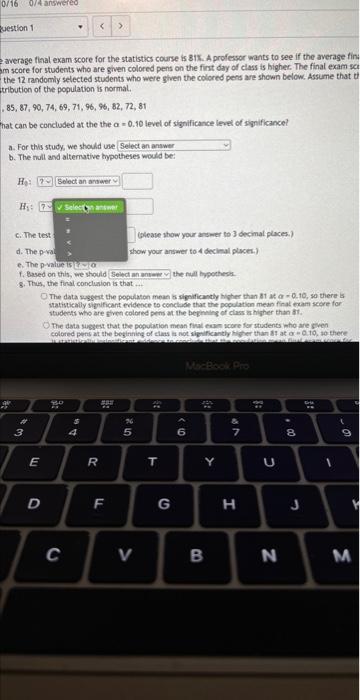The data suggest that the population mean final exam score for students who are given colored pens at the beginning of class is not significantly higher than 81 at \( \alpha=0.10 \), so there le average final exam score for the statistics course is \( 81 \% \). A professor wants to see if the average final iam score for students who are given colored pens on the first day of class is higher. The final exam scores \( r \) the 12 randomly selected students who were given the colored pens are shown below. Assume that the stribution of the population is normal. \( 1,85,87,90,74,69,71,96,96,82,72,81 \) That can be concluded at the the \( \alpha=0.10 \) level of significance level of significance? a. For this study, we shouts use b. The null and alternative hypotheses would be: c. The test statistic \( \quad=\quad \) (please show your answer to 3 decimal places.) d. The \( p \)-value \( =\quad \) (Please show your answer to 4 decimal places.) e. The p-value is \( \alpha \) f. Based on this, we should the null hypothesis. 8. Thus, the final conclusion is that ... The data suggest the populaton mean is significantly higher than 81 at \( \alpha=0.10 \), so there is statistically significant evidence to conclude that the population mean final exam score for students who are given colored pens at the beginning of class is higher than 81. The data suggest that the population mean final exam score for students who are given colored pens at the beginning of class is not significantly higher than 81 at \( \alpha=0.10 \), so there he average final exam score for the statistics course is 813. A professor wants to see if the average finat aam score for students who are given colored pens on the first day of class is higher. The final exam scores or the 12 randomly selected students who were given the colored pens are shown below. Assume that the istribution of the population is normal. \[ 91,85,87,90,74,69,71,96,96,82,72,81 \] What can be concluded at the the \( a=0.10 \) level of significance level of significance? a. For this study, we should use b. The null and alternative hypotheses wound be: d. The p-value = (Please show your arower to 4 decimat places) e. The p-value is \( \alpha \) 1. Based on this, we thould g. Thas, the final conclusion is that The data suggest the populatoe mean is slignificantly higher than 81 at \( \alpha=0 \). 10, so there \( b \) statistically significant evidence to conclude that the population mean final exam score for students who are given colored pens at the berineing of class is higher than 81 . 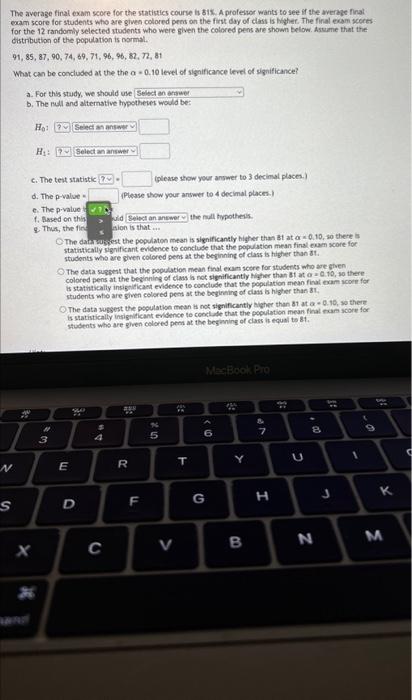The data suggest that the popuilation mean final exam score for students who are given colored pens at the beginning of class is not significantly higher than 81 at \( \alpha=0.10 \), so there e average final exam score for the statistics course is \( 81 \% \). A professor wants to see if the average am score for students who are given colored pens on the first day of class is higher. The final exam r the 12 randomly selected students who were given the colored pens are shown below. Assume that stribution of the population is normal. \[ 9,85,87,90,74,69,71,96,96,82,72,81 \] What can be concluded at the the \( \alpha=0,10 \) level of significance level of significance? a. For this study, we should use b. The eull and alternative typotheses would be: \( H_{0} \) : d. The p-yalue = (Please show your answer to 4 decienal places.) e. The p-value is f. Dased on this, we should the mull hypothesis. 8. Thus, the final conchusion is that .... The data suggest the populaton mean is sigaificantly hipher than 81 at \( \alpha=0.10 \), so there is statiatically signiticant evidence to conclude that the population mean final exam score for students who are given colored pens at the beginning of class is higher than \&?. The data sugsest that the population mean finat exam score for itudents who are given colored pens at the beginning of class is not significantly higer than 81 at a \( + \) a. 10, so there 2werage final exam score for the statistics course is 31x. A professor wants to see if the average fini m score for students who are given colored pens on the first day of class is higher. The final exam son the 12 randomly selected students who were given the colored pers are shown below. Assume that if tribution of the pogulation is normal. \[ 85,87,90,74,69,71,96,96,82,72,81 \] that can be concluded at the the \( \alpha=0.10 \) level of significance ievel of significance? a. For this study, we should use: b. The null and alterrative typotheses would be: \[ \mathrm{H}_{0}=20 \] c. The test : Glease show your ansmer to 3 decimal places.) d. The p-ial how your answer to 4 decimal places.) e. The p-vanue ws z \( x \) o 1. Based on this, we should 3. Thus, the final concluaion is that ... The data msgert the popolaton mean is slgnificantly higher than 81 at \( \alpha=0.10 \), so there is suatistically significart edidence to concluse that the pooviation mein finat ecam score for studeets who are sivet colored pens at the begheing of class a higher than it. 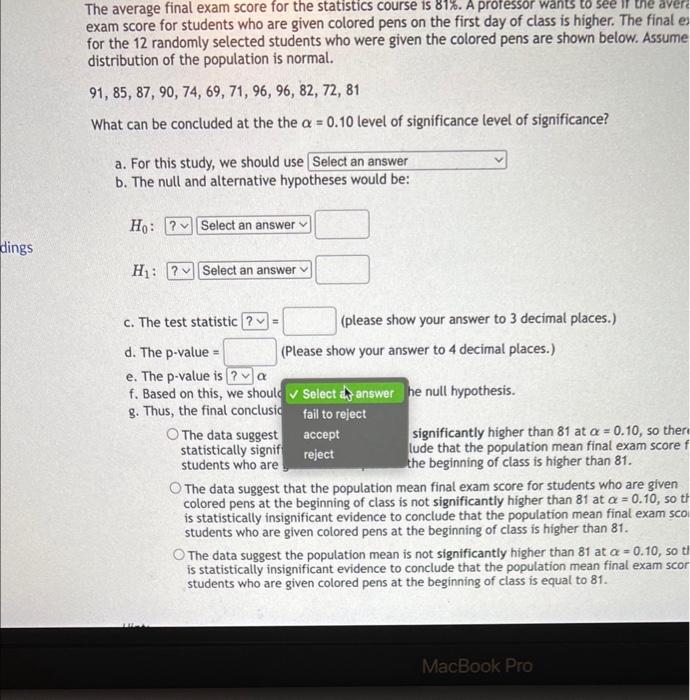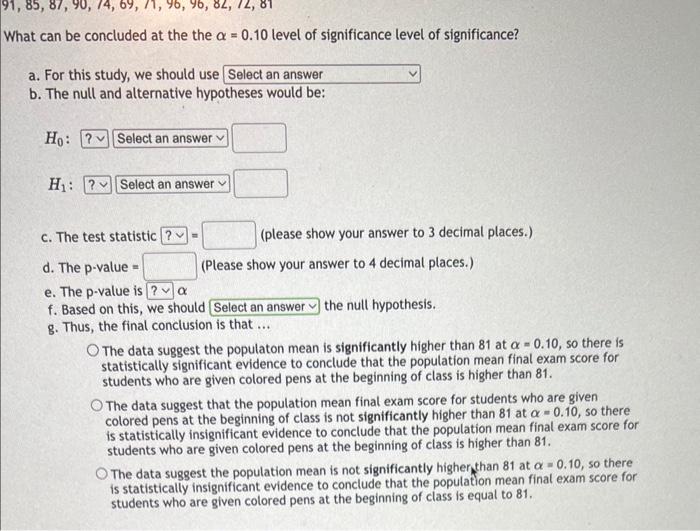The data sugsest that the popviarion mean fival eaxn vcore for students who are swen colored pers at the beginnieg of class it not sipificantly tister than it at a \( =0 \) to, so thece erage final exam score for the statistics course is \( 81 \% \). A professor wants to see if the average final score for students who are given colored pens on the first day of class is higher. The final exam scores 12 randomly selected students who were given the colored pens are shown below. Assume that the bution of the population is normal. \[ 5,87,90,74,69,71,96,96,82,72,81 \] can be concluded at the the \( \alpha=0,10 \) level of significance level of significance? For this study, we should use The null and alternative hypotheses would be: \( H_{0} \) : \( \mathrm{H}_{1} \) : c. The test statistid (please show your answer to 3 decimal places.) d. The p-value = (Please show your answer to 4 decimal places.) e. The p-value is f. Based on this, we should g. Thus, the final conclusion is that ... The data suggest the populaton mean is significantly higher than 81 at \( \alpha=0.10 \), so there is statistically significant evidence to conclude that the population mean final exam score for students who are given colored pens at the beginning of class is higher than 81 . The data suggest that the population mean final exam score for students who are given colored pens at the beginning of class is not significantly higher than 81 at \( \alpha=0.10 \), so there is statistically insignificant evidence to conclude that the population mean final exam score for students who are given colored pens at the beginning of class is higher than 81 . The data suggest the population mean is not significantly higher than 81 at \( \alpha=0.10 \), so there is statistically insignificant evidence to conclude that the population mean finat exam score for students who are given colored pens at the beginning of class is equal to 81 . The average final exam score for the statistics course is b31. A profeltor wants to see if the average finat earam score for students who are given colored pees an the first day of class is higher. The firal exam sceces for the 12 randomily selected students who were given the colored pens are shown tellow. Assume that the distribution of the population is normal. \[ 91,85,87,90,74,69,71,96,96,82,72,81 \] What can be concluded at the the \( \alpha=0.10 \) level of sigaificance terel of significance? a. For this stady, we thould use b. The mell and altemative hypotneres wous oer \( \mathrm{H}_{1}: \) c. The test statistic (gieace thow your answer to 3 decimal places.) d. The p-value = e. The p-value t 1. Aased on thit Nid the null brpotheris. 9. Thur, the fir. sion is that The datimubrest the populaton mean is significantly higher than 31 at a a \( 0.10,30 \) thete 3 statistically rigrificant evidence to conchude that the population mean final easen score for students who are given colored pens at the beginning of class is higher than d1. The cata sugsent that the population mean fingl exam score for students who age given colored pens at the beginning of class ia not significantiy bigher than Bt at of a \( 0.10 \), so there is statiticalty insig-liticact eviseoce to conclude that the pooulation mean final carm icoet for students who are given colored peed at the begireing of class b higher than st. The data wugsest the population mean it noc significantly aigher than 81 at \( a+0.10,30 \) there is statistically insigriticant evisence to concluse that the population thean fhal ruan score for studeats who are plien celored pert at the begining of class is equal to 81 . The average final exam score for the statistics course is \( 81 \% \). A professor wants to see in the aver exam score for students who are given colored pens on the first day of class is higher. The final for the 12 randomly selected students who were given the colored pens are shown below. Assume distribution of the population is normal. \[ 91,85,87,90,74,69,71,96,96,82,72,81 \] What can be concluded at the the \( \alpha=0.10 \) level of significance level of significance? a. For this study, we should use b. The null and alternative hypotheses would be: \( H_{0} \) : \( H_{1} \) : c. The test statistic \( \quad=\quad \) (please show your answer to 3 decimal places.) d. The \( \mathrm{p} \)-value \( =\quad \) (Please show your answer to 4 decimal places.) e. The \( \mathrm{p} \)-value is \( \alpha \) f. Based on this, we shoulc g. Thus, the final conclusic The data suggest significantly higher than 81 at \( \alpha=0.10 \), so ther statistically signif lude that the population mean final exam score students who are he beginning of class is higher than 81 . The data suggest that the population mean final exam score for students who are given colored pens at the beginning of class is not significantly higher than 81 at \( \alpha=0.10 \), so t is statistically insignificant evidence to conclude that the population mean final exam sco students who are given colored pens at the beginning of class is higher than 81 . The data suggest the population mean is not significantly higher than 81 at \( \alpha=0.10 \), so t is statistically insignificant evidence to conclude that the population mean final exam scon students who are given colored pens at the beginning of class is equal to 81 . can be concluded at the the \( \alpha=0.10 \) level of significance level of significance? a. For this study, we should use b. The null and alternative hypotheses would be: \( H_{0} \) : \( H_{1} \) : c. The test statistic (please show your answer to 3 decimal places.) d. The p-value \( = \) (Please show your answer to 4 decimal places.) e. The \( p \)-value is \( \alpha \) f. Based on this, we should g. Thus, the final conclusion is that ... The data suggest the populaton mean is significantly higher than 81 at \( \alpha=0.10 \), so there is statistically significant evidence to conclude that the population mean final exam score for students who are given colored pens at the beginning of class is higher than 81. The data suggest that the population mean final exam score for students who are given colored pens at the beginning of class is not significantly higher than 81 at \( \alpha=0.10 \), so there is statistically insignificant evidence to conclude that the population mean final exam score for students who are given colored pens at the beginning of class is higher than 81 . The data suggest the population mean is not significantly higher than 81 at \( \alpha=0.10 \), so there is statistically insignificant evidence to conclude that the population mean final exam score for students who are given colored pens at the beginning of class is equal to 81 .