(Solved): Suppose we are interested in studying a population to estimate its mean. The population is normal a ...

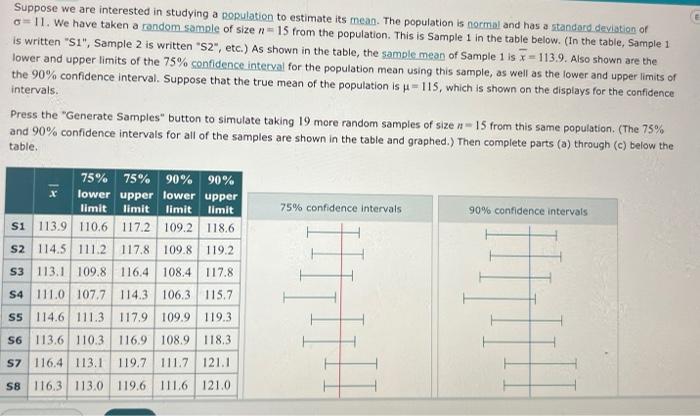
Suppose we are interested in studying a population to estimate its mean. The population is normal and has a standard deviation of \( \sigma=11 \). We have taken a random sample of size \( n=15 \) from the population. This is Sample 1 in the table below. (In the table, Sample 1 is written "S1", Sample 2 is written "S2", etc.) As shown in the table, the sample mean of Sample 1 is \( \bar{x}=113.9 \). Also shown are the lower and upper limits of the \( 75 \% \) confidence interval for the population mean using this sample, as well as the lower and upper limits of the \( 90 \% \) confidence interval. Suppose that the true mean of the population is \( \mu=115 \), which is shown on the displays for the confidence intervals. Press the "Generate Samples" button to simulate taking 19 more random samples of size \( n=15 \) from this same population. (The \( 75 \% \) and \( 90 \% \) confidence intervals for all of the samples are shown in the table and graphed.) Then complete parts (a) through (c) below the table. 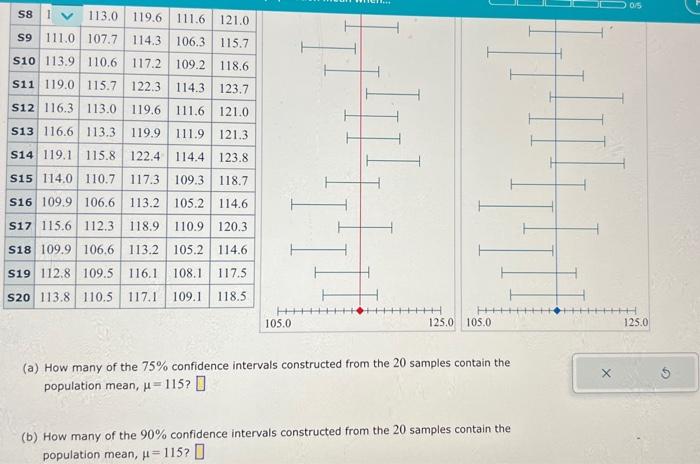(a) How many of the \( 75 \% \) confidence intervals constructed from the 20 samples contain the population mean, \( \mu=115 \) ? (b) How many of the \( 90 \% \) confidence intervals constructed from the 20 samples contain the population mean, \( \mu=115 \) ? (c) Choose ALL that are true. For some of the samples, the \( 75 \% \) confidence interval is included in the \( 90 \% \) confidence interval, while for other samples, this is not the case. It is not surprising that some \( 75 \% \) confidence intervals are different from other \( 75 \% \) confidence intervals. Each confidence interval depends on its sample, and different samples may give different confidence intervals. The sample means for Sample 19 and Sample 20 are different, so the center of the \( 90 \% \) confidence interval for Sample 19 is different from the center of the \( 90 \% \) confidence interval for Sample 20. We would expect to find more \( 75 \% \) confidence intervals that contain the population mean than \( 90 \% \) confidence intervals that contain the population mean. Given a sample, a higher confidence level results in a narrower interval. None of the choices above are true.