(Solved): Suppose that Raley is a diligent second-year college student, One Wednosday, she decides to start t ...

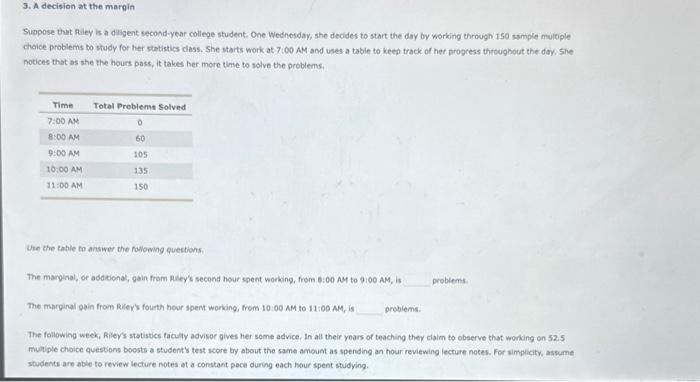
Suppose that Raley is a diligent second-year college student, One Wednosday, she decides to start the day by working through 150 sample multiple chaice problems to study for her watistics class. She starts work at. 7100 AM and uses a table to keep track of her progress throughout the doy. She notices that as she the hours pass, it takes her more time to solve the problems, Vhe the table to answer the following quections. The marginal, or additional, gain from Aley's second hour spent working, from B:00 AM to 9:00 AM, is The marginal gain from Riler's fourth hour spent working, from \( 10: 00 \mathrm{AM} \) to \( 11: 00 \mathrm{AM} \), is problems. The following week, Rller's statistics facuty advisor gives her some advice. In all their years of teaching they ciaim to observe that working on \( 52.5 \). muliple choice questions boosts a student's test score by about the same amount as spending an hour reviewing lecture notes. For simplicity, assume students are able to roview lecture notes at a constant pace during each hour spent studying. 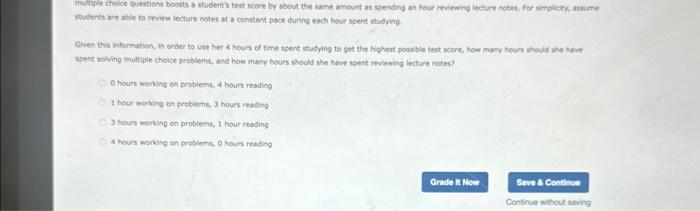students are bble to review lecturn notes at a constant poce during each hour spent studying. Elven this information, in order to use her 4 hours of time spent studying to get the highest possble test score. Now many hours should she Auvt Npenk nolving inultiple choice problems, and how muny nours should she have spent reviewing lecture notes? O houn working on problems, 4 hours reading I hour narking on problems, 3 hours readitg 3 houn working on problems, I hsur resding 4 hours working on problems, 0 hours reading