(Solved): Suppose \( A \) and \( B \) are two non-singular matrices. \( \left(A^{T} \cdot B\right)^{-1} \) is ...

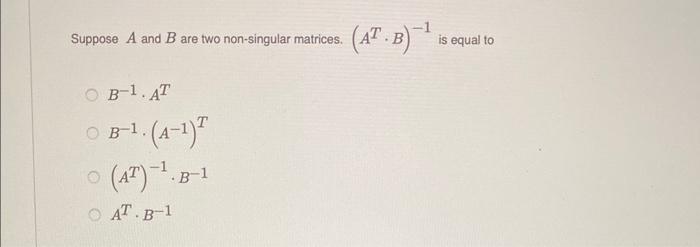
Suppose \( A \) and \( B \) are two non-singular matrices. \( \left(A^{T} \cdot B\right)^{-1} \) is equal to \[ \begin{array}{l} B^{-1} \cdot A^{T} \\ B^{-1} \cdot\left(A^{-1}\right)^{T} \\ \left(A^{T}\right)^{-1} \cdot B^{-1} \\ A^{T} \cdot B^{-1} \end{array} \]