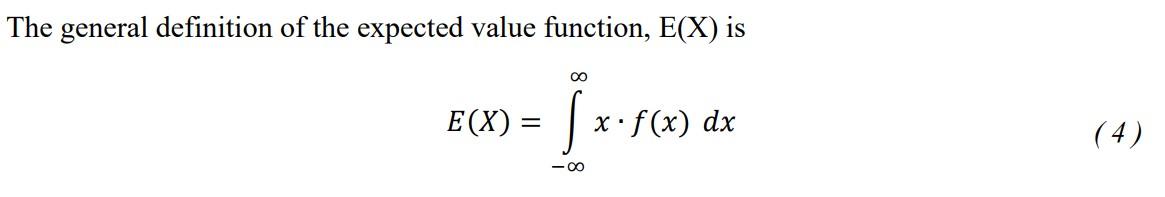(Solved): Subproblem 1(d) For our Uniform random variable \( V \), derive the expected value for \( V^{2} \) ...

Subproblem 1(d) For our Uniform random variable \( V \), derive the expected value for \( V^{2} \), i.e.: \[ E\left(V^{2}\right) \] Hint: Start with equation ( 4 ) by exchanging \( v \) for \( v^{2} \), but without affecting \( f(v) \) because the probability density of \( V \) was not fundamentally changed (i.e. the underlying process(es) generating values of \( v \) was not altered). The general definition of the expected value function, \( \mathrm{E}(\mathrm{X}) \) is \[ E(X)=\int_{-\infty}^{\infty} x \cdot f(x) d x \]