(Solved): SOLVE USING LAPLACE TRANSFORM FORMULAS. I included an attachment of the laplace transform tables 2. ...

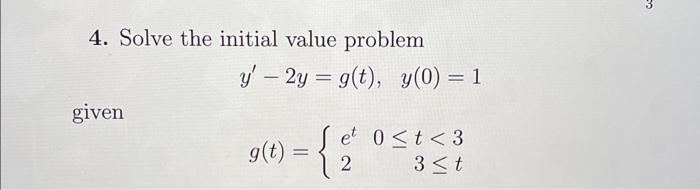
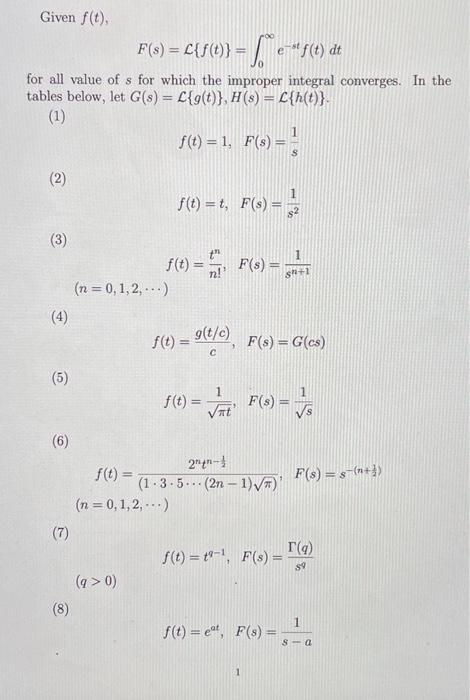
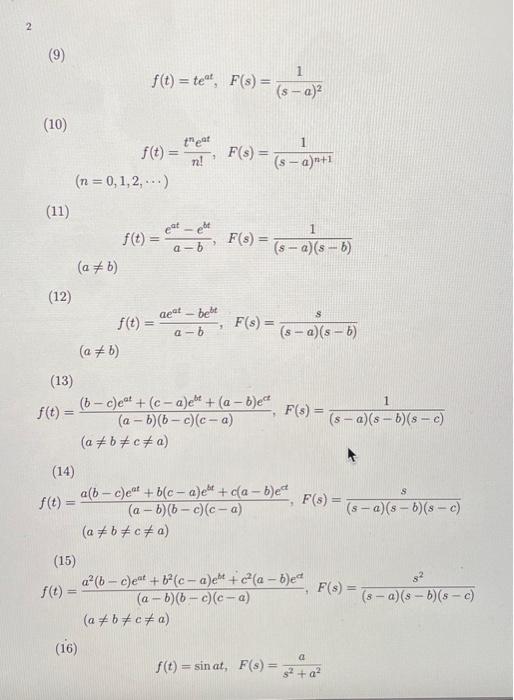
2. Solve the initial value problem $4y^{??}+y=U(t??),y(0)=1,y^{?}(0)=0$ Note: The angle addition formulas on page 8 of the additional formulas sheet may be useful.] 4. Solve the initial value problem $y^{?}?2y=g(t),y(0)=1$ given $g(t)=\{\begin{array}{lr}{e}^t& 0?t<3\\ 2& 3?t\end{array}$ Given $f(t)$, $F(s)=\mathcal{L}\{f(t)\}={?}_0^{?}{e}^{?st}f(t)dt$ for all value of $s$ for which the improper integral converges. In the tables below, let $G(s)=\mathcal{L}\{g(t)\},H(s)=\mathcal{L}\{h(t)\}$. (1) $f(t)=1,F(s)=\frac{1}{s}$ (2) $f(t)=t,F(s)=\frac{1}{s^2}$ (3) $\begin{array}{l}f(t)=\frac{t^n}{n!},F(s)=\frac{1}{s^{n+1}}\\ (n=0,1,2,?)\end{array}$ (4) $f(t)=\frac{g(t/c)}{c},F(s)=G(cs)$ (5) $f(t)=\frac{1}{\sqrt{?t}},F(s)=\frac{1}{\sqrt{s}}$ (6) $\begin{array}{l}f(t)=\frac{2^n{t}^{n?\frac{1}{2}}}{(1?3?5?(2n?1)\sqrt{?})},F(s)=s^{?\left(n+\frac{1}{2}\right)}\\ (n=0,1,2,?)\end{array}$ (7) $f(t)=t^{q?1},F(s)=\frac{?(q)}{s^q}$ $(q>0)$ (8) $f(t)=e^{at},F(s)=\frac{1}{s?a}$ (9) $f(t)=t{e}^{at},F(s)=\frac{1}{(s?a{)}^2}$ (10) $\begin{array}{l}f(t)=\frac{t^n{e}^{at}}{n!},F(s)=\frac{1}{(s?a{)}^{n+1}}\\ (n=0,1,2,?)\end{array}$ (11) $f(t)=\frac{e^{at}?e^{bt}}{a?b},F(s)=\frac{1}{(s?a)(s?b)}$ $(a?=b)$ (12) $\begin{array}{l}f(t)=\frac{a{e}^{at}?b{e}^{bt}}{a?b},F(s)=\frac{s}{(s?a)(s?b)}\\ (a?=b)\end{array}$ (13) $\begin{array}{rl}f(t)=& \frac{(b?c)e^{at}+(c?a)e^{bt}+(a?b)e^{ct}}{(a?b)(b?c)(c?a)},F(s)=\frac{1}{(s?a)(s?b)(s?c)},\\ & (a?=b?=c?=a)\end{array}$ (14) $\begin{array}{rl}f(t)=& \frac{a(b?c)e^{at}+b(c?a)e^{bt}+c(a?b)e^{ct}}{(a?b)(b?c)(c?a)},F(s)=\frac{s}{(s?a)(s?b)(s?c)}\\ & (a?=b?=c?=a)\end{array}$ (15) $\begin{array}{rl}f(t)=& \frac{a^2(b?c)e^{at}+b^2(c?a)e^{ht}+c^2(a?b)e^d}{(a?b)(b?c)(c?a)},F(s)=\frac{s^2}{(s?a)(s?b)(s?c)}\\ & (a?=b?=c?=a)\end{array}$ (16) $f(t)=\sin at,F(s)=\frac{a}{s^2+a^2}$ (17) $f(t)=\cos at,F(s)=\frac{s}{s^2+a^2}$ $(18)$ $f(t)=\sin (at+b),F(s)=\frac{s\sin b+a\cos b}{s^2+a^2}$ (19) $f(t)=\cos (at+b),F(s)=\frac{s\cos b?a\sin b}{s^2+a^2}$ $(20)$ $f(t)=\text{ sinhat, }F(s)=\frac{a}{s^2?a^2}$ $f(t)=\cosh at,F(s)=\frac{s}{s^2?a^2}$ $f(t)=\frac{1?\cos at}{a^2},F(s)=\frac{1}{s\left(s^2+a^2\right)}$ (23) $f(t)=\frac{at?\sin at}{a^3},F(s)=\frac{1}{s^2\left(s^2+a^2\right)}$ $(24)$ $f(t)=\frac{\sin at?at\cos at}{2a^3},F(s)=\frac{1}{{\left(s^2+a^2\right)}^2}$ $(25)$ $f(t)=\frac{t\sin at}{2a},F(s)=\frac{s}{{\left(s^2+a^2\right)}^2}$ $(26)$ $f(t)=\frac{\sin at+at\cos at}{2a},F(s)=\frac{s^2}{{\left(s^2+a^2\right)}^2}$ $f(t)=t\cos at,F(s)=\frac{s^2?a^2}{{\left(s^2+a^2\right)}^2}$ (28) $f(t)=\frac{(1/a)\sin at?(1/b)\sin bt}{b^2?a^2},F(s)=\frac{1}{\left(s^2+a^2\right)\left(s^2+b^2\right)}$ (29) $\begin{array}{l}f(t)=\frac{\cos at?\cos bt}{b^2?a^2},F(s)=\frac{s}{\left(s^2+a^2\right)\left(s^2+b^2\right)}\\ \left(a^2?=b^2\right)\end{array}$ $(30)$ $f(t)=e^{at}\sin bt,F(s)=\frac{b}{(s?a{)}^2+b^2}$ $(31)$ $f(t)=e^{at}\cos bt,F(s)=\frac{s?a}{(s?a{)}^2+b^2}$ $(32)$ $f(t)=e^{at}\left(\cos bt+\frac{a}{b}\sin bt\right),F(s)=\frac{s}{(s?a{)}^2+b^2}$ (33) $f(t)=\frac{a{e}^{at}\sin bt?b{e}^{at}\cos bt+b}{a^2+b^2},F(s)=\frac{b}{s\left((s?a{)}^2+b^2\right)}$ $(34)$ $f(t)=\frac{\left(a^2?b^2\right)e^{at}\sin bt?2ab{e}^{at}\cos bt}{{\left(a^2+b^2\right)}^2}+\frac{bt+2ab}{a^2+b^2},F(s)=\frac{b}{s^2\left((s?a{)}^2+b^2\right)}$ $(35)$ $f(t)=U(t?c)=\{\begin{array}{ll}0& x<c\\ 1& x?c\end{array},F(s)=\frac{e^{?c}}{s}$ $(36)$ $f(t)=g^{?}(t),F(s)=sG(s)?g\left(0^{+}\right)$ $[g\left(0^{+}\right)$means ${\lim }_{t?0^{+}}g(t)$, which is the same as $g(0)$ when $g$ is continuous at 0 .] (37) $f(t)=g^{??}(t),F(s)=s^{2}G(s)?sg\left(0^{+}\right)?g^{?}\left(0^{+}\right)$ (38) $f(t)=g^{(n)}(t),F(s)=s^{n}G(s)?s^{n?1}g\left(0^{+}\right)?\dots ?g^{(n?1)}\left(0^{?}\right)$ $(39)$ $f(t)=e^{at}g(t),F(s)=G(s?a)$ (40) $f(t)=U(t?c)g(t?c),F(s)=e^{?cs}G(s)$ $(41)$ $f(t)=U(t?c)g(t),F(s)=e^{?c}\mathcal{L}\{g(t+c)\}$ $(42)$ $f(t)={?}_0^{t}g(u)du,F(s)=\frac{G(s)}{s}$ $(43)$ $f(t)=\mathrm{tg}(t),F(s)=?G^{?}(s)$ $(44)$ $f(t)=(?1{)}^n{t}^{n}g(t),F(s)=G^{(n)}(s)$ (45) $f(t)=g?h(t)={?}_0^{t}g(t?u)h(u)du,F(s)=G(s)H(s)$ $(46)$ $f(t)=\frac{g(t)}{t},F(s)={?}_0^{?}G(u)du$