(Solved): Solve the following system using augmented matrix methods: \[ \begin{array}{c} -4 x_{1}+5 x_{2}-4 ...

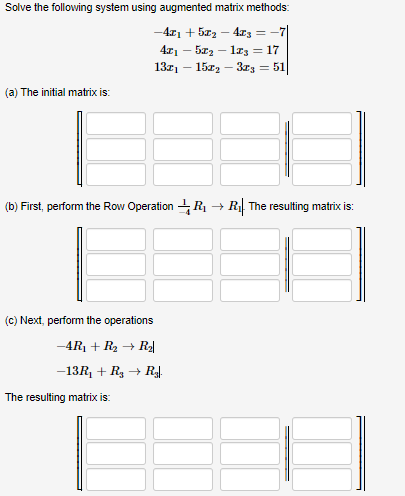
Solve the following system using augmented matrix methods: \[ \begin{array}{c} -4 x_{1}+5 x_{2}-4 x_{3}=-7 \\ 4 x_{1}-5 x_{2}-1 x_{3}=17 \\ 13 x_{1}-15 x_{2}-3 x_{3}=51 \end{array} \mid \] (a) The initial matrix is: (b) First, perform the Row Operation \( \frac{1}{-4} R_{1} \rightarrow R_{1} \). The resulting matrix is: (c) Next, perform the operations \[ \begin{array}{l} -4 R_{1}+R_{2} \rightarrow R_{2} \mid \\ -13 R_{1}+R_{3} \rightarrow R_{3} . \end{array} \] The resulting matrix is: (d) Finish simplifying the augmented matrix down to reduced row echelon form. The reduced matrix is: Remember: This matrix must be simplified all the way to reduced form. (e) How many solutions does the system have? If infinitely many, enter "Infinity". (f) What are the solutions to the system? \[ \begin{array}{l} x_{1}= \\ x_{2}= \\ x_{3}= \end{array} \] Note: If there are no solutions, write "No Solution" or "None" for each answer. If there are infinitely many solutions, and the solution set describes a line (that is, if there is only one free variable), set \( x_{2}=\not \) and solve for the remaining variables in terms of \( t \) If there are infinitely many solutions, and the solution set describes a plane (that is, if the solution set has two free variables), set the variables \( x_{3}=t \) and \( x_{2}=s \) and then solve for \( x_{1} \mid \) in terms of \( s \) and \( t \)