So we are learning about the VC Dimension. This comes from our book: Introduction to Machine Learning, 4th Edition by Ethan Alpaydin. Here is the following info we are given about VC Dimension:We are also given the following figure:This is Figure 2.6. Caption for this figure: An axis-aligned rectangle can shatter 4 points. Only rectangles covering solutionspile.com

Question

So we are learning about the VC Dimension. This comes from our book: Introduction to Machine Learning, 4th Edition by Ethan Alpaydin. Here is the following info we are given about VC Dimension:
student submitted image, transcription available below

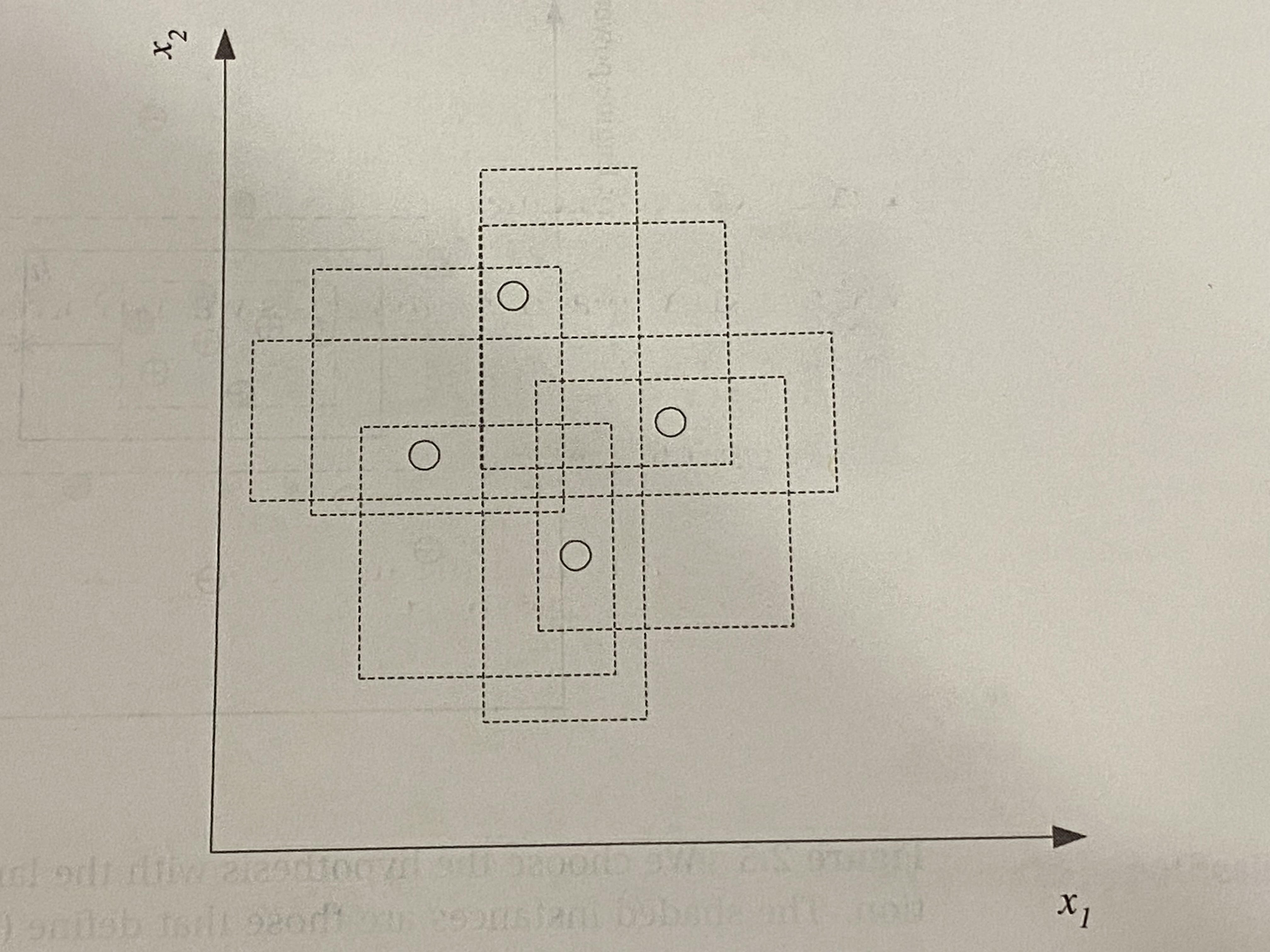
We are also given the following figure:

This is Figure 2.6. Caption for this figure: An axis-aligned rectangle can shatter 4 points. Only rectangles covering 2 points are shown.

My question is: How would we go about finding the Breakpoint and Growth Function for this figure? The hypothesis class H, according to the book, is the hypothesis class of axis-aligned rectangles in 2 Dimensions. The VC (H) for this figure is 4. So 4 points can be shattered. I am also not understanding how the VC is 4. Would greatly appreciate an explanation and answer on this!

Vapnik-Chervonenkis Dimension Let us say we have a dataset containing

N

points. These

N

points can be labeled in

2^{N}

ways as positive and negative. Therefore,

2^{N}

different learning problems can be defined by

N

data points. If for any of these problems, we can find a hypothesis

h ? H

that separates the positive examples from the negative, then we say

H

shatters

N

points. That is, any learning problem definable by

N

examples can be learned with no error by a hypothesis drawn from

H

. The maximum number of points that can be shattered by

H

is called the Vapnik-Chervonenkis (VC) dimension of

H

is denoted as

VC (H)

, and measures the capacity of

H

.

Accepted Answer

Expert Answer to - So we are learning about the VC Dimension. This comes from our book: Introduction to Machine Learnin

Answer

Solution for - So we are learning about the VC Dimension. This comes from our book: Introduction to Machine Learnin

Answer

This an additional answer to - So we are learning about the VC Dimension. This comes from our book: Introduction to Machine Learnin

(Solved): So we are learning about the VC Dimension. This comes from our book: Introduction to Machine Learnin ...

View Expert Answer

Expert Answer

Buy This Answer $5

Place Order

We Provide Services Across The Globe