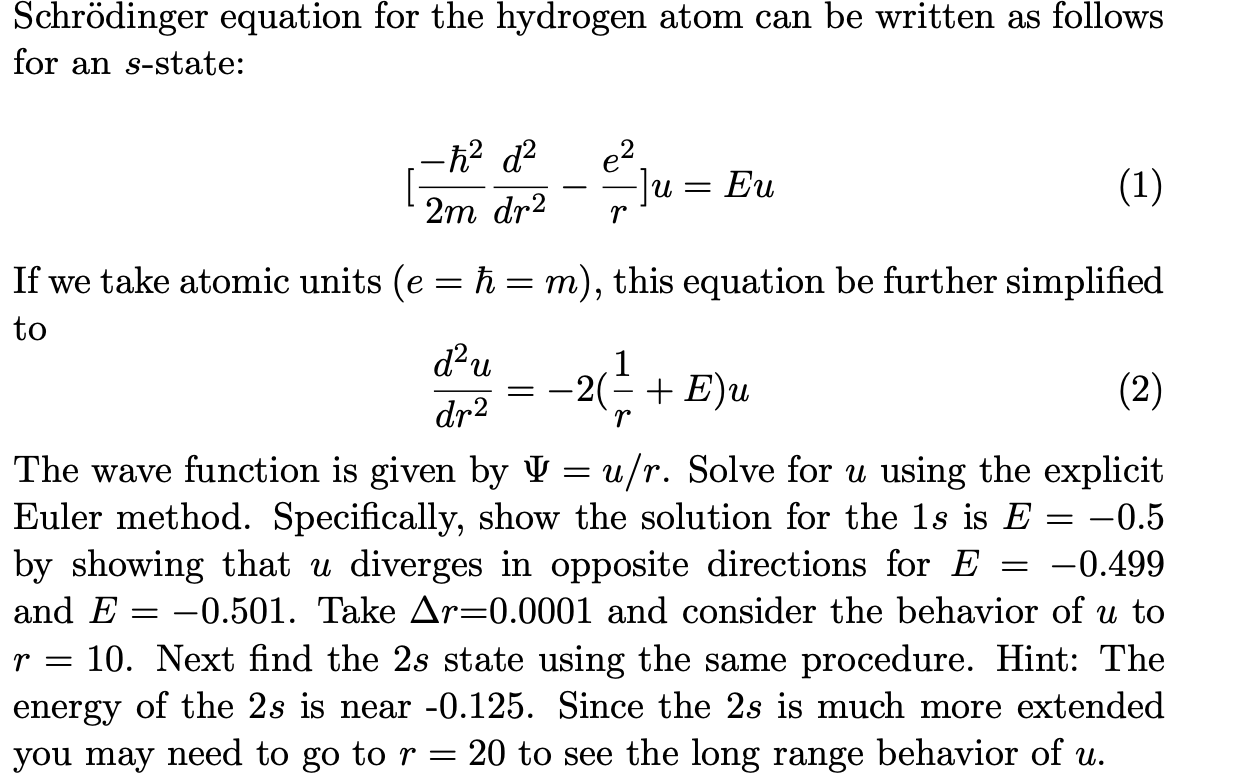(Solved): Schrdinger equation for the hydrogen atom can be written as follows for an \( s \)-state: \[ \le ...

Schrödinger equation for the hydrogen atom can be written as follows for an \( s \)-state: \[ \left[\frac{-\hbar^{2}}{2 m} \frac{d^{2}}{d r^{2}}-\frac{e^{2}}{r}\right] u=E u \] If we take atomic units \( (e=\hbar=m) \), this equation be further simplified to \[ \frac{d^{2} u}{d r^{2}}=-2\left(\frac{1}{r}+E\right) u \] The wave function is given by \( \Psi=u / r \). Solve for \( u \) using the explicit Euler method. Specifically, show the solution for the \( 1 s \) is \( E=-0.5 \) by showing that \( u \) diverges in opposite directions for \( E=-0.499 \) and \( E=-0.501 \). Take \( \Delta r=0.0001 \) and consider the behavior of \( u \) to \( r=10 \). Next find the \( 2 s \) state using the same procedure. Hint: The energy of the \( 2 s \) is near \( -0.125 \). Since the \( 2 s \) is much more extended you may need to go to \( r=20 \) to see the long range behavior of \( u \).