Home /
Expert Answers /
Advanced Math /
s6-i-can-state-and-prove-that-the-infinite-intersection-an-d-o-r-union-of-sets-is-equal-to-a-set-pa453
(Solved): S6. I can state and prove that the infinite intersection an(d)/(o)r union of sets is equal to a set. ...
S6. I can state and prove that the infinite intersection
an(d)/(o)r union of sets is equal to a set.
In this take-home, we will [hopefully] learn how to understand infinite intersections and unions of
sets. First, we need to understand what the unio(n)/(i)ntersection of more than two sets look like.
First, recall that we define the union and intersection of two sets as
A\cup B={x:xinA OR xinB}, and ,A\cap B={x:xinA AND xinB}
We can extend these definition to more than two sets in exactly the way that you'd expect:
\cup u_(i)=1^(n)A_(i)=A_(1)\cup A_(2)\cup A_(3)\cup cdots\cup A_(n)={x:xinA_(i) for at least one of the i}
and
\cap n_(i)=1^(n)A_(i)=A_(1)\cap A_(2)\cap A_(3)\cap cdots\cap A_(n)={x:xinA_(i) for all of the i}
Notice the new notation \cap n_(i)=1^(n)A_(i) and \cup u_(i)=1^(n)A_(i), which are similar to some notation you may have seen
for sums \sum or products prodi=1 from calculus. Let's consider an example:
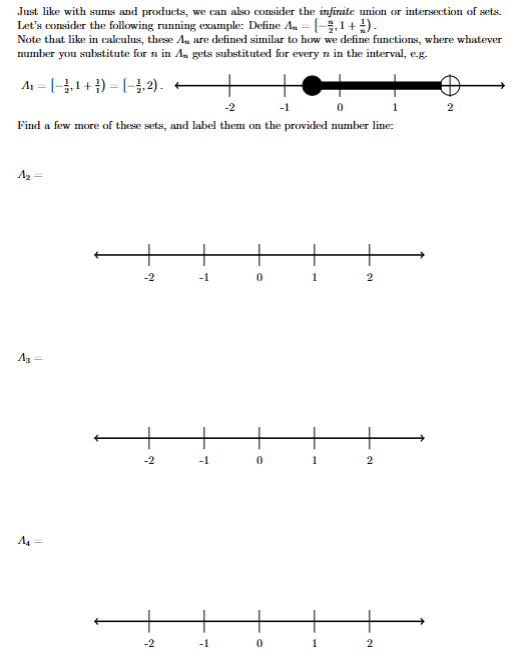
Example 0.2. Suppose , Just like with sums and products, we can also consider the infinite union or intersection of sets.
Let's consider the following running example: Define \Lambda _(n)=[-(n)/(2),1+(1)/(n)).
Note that like in calculus, these A_(n) are defined similar to how we define functions, where whatever
number you substitute for n in \Lambda _(n) gets substituted for every n in the interval, e.g.
\Lambda _(1)=
Find a few more of these sets, and label them on the provided number line:
\Lambda _(2)=
A_(3)=
\Lambda _(4)=