(Solved): Roll two fair dice. Each die has six faces. - Let A be the event that either a 3 or 4 is rolled fir ...

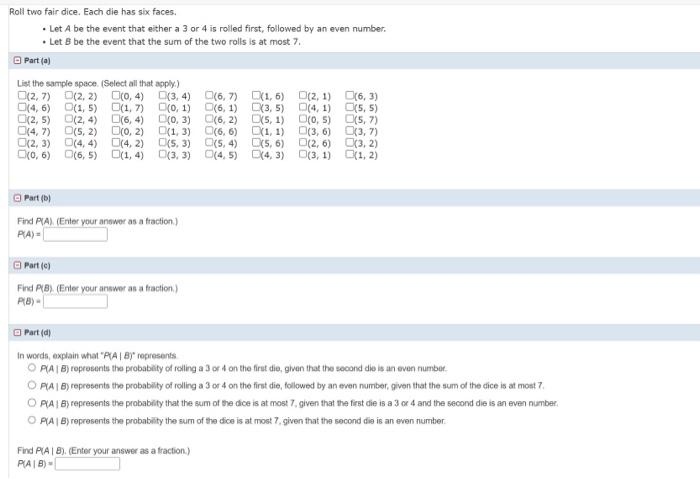
Roll two fair dice. Each die has six faces. - Let $A$ be the event that either a 3 or 4 is rolled first, followed by an even number. - Let $B$ be the event that the sum of the two rolls is at most 7 . Part (a) List the sample space. (Select all that apply.) \begin{tabular}{llrlllll} $(2,7)$ & $2,2)$ & $?(0,4)$ & $?(3,4)$ & $?(6,7)$ & $?(1,6)$ & $?(2,1)$ & $?(6,3)$ \\ $(4,6)$ & $(1,5)$ & $(1,7)$ & $?(0,1)$ & $?(6,1)$ & $?(3,5)$ & $?(4,1)$ & $?(5,5)$ \\ $(2,5)$ & $(2,4)$ & $(6,4)$ & $?(0,3)$ & $?(6,2)$ & $?(5,1)$ & $?(0,5)$ & $?(5,7)$ \\ $(4,7)$ & $(5,2)$ & $(0,2)$ & $?(1,3)$ & $?(6,6)$ & $?(1,1)$ & $?(3,6)$ & $?(3,7)$ \\ $(2,3)$ & $(4,4)$ & $(4,2)$ & $?(5,3)$ & $?(5,4)$ & $?(5,6)$ & $?(2,6)$ & $?(3,2)$ \\ $(0,6)$ & $(6,5)$ & $(1,4)$ & $?(3,3)$ & $?(4,5)$ & $?(4,3)$ & $?(3,1)$ & $?(1,2)$ \end{tabular} Part (b) Find $P(A)$, (Enter your anower as a fraction.) $P(A)=$ Part (c) Find $P(B)$. (Enter your answer as a fraction.) $P(B)=$ Part (d) In words, explain what " $P(A?B)$ " represents $A(A?B)$ ropresents the probabilty of roiling a 3 of 4 on the firat die, given that the second die is an even number. PA $?$ B) represents the probability of rolling a 3 or 4 on the first die, followed by an even number, given that the sum of the dice is at most 7 . $A(A?B)$ represents the probabilty that the sum of the dice is at most 7 , given that the frest die is a $3?4$ and the second die is an even number. $P(A?B)$ represents the probability the sum of the dice is at most 7 , given that the second die is an even rumber. Find $P(A?B)$. (Enter your answer as a fraction) $P(A?B)=$ Are $A$ and $B$ mulually exclusive events? Explain your answer. The events are mutually exclustve. Rolling 4, 6 is an outcome in event $A$ but not in event $B$. The events are not mutually exclusive. Rolling 3,2 is an outcome in event $A$ and also an outcome in event $B$. The events are mutually exclusive. Rolling 3,2 is an cutcome in event $A$ and also an outcome in event $B$. The events are not mutually exclusive. Roling 4,6 is an outcome in evert $A$ but not in event $B$. Part (f) Are $A$ and $B$ independent events? Explain your answer. Events $A$ and $B$ are dependent because they have outcomes in common. Events $A$ and $B$ are independent because they are mutually exclusive. Events $A$ and $B$ are independent because the roll of one die has no effect on the outcome of rolling a second die. Events $A$ and $B$ are dependent because tho probabilfy of event $A$ happening is affected by whether event $B$ has happened.