(Solved): RLAT-8n Consider root locus of a unity feedback system with the following open loop transfer funct ...

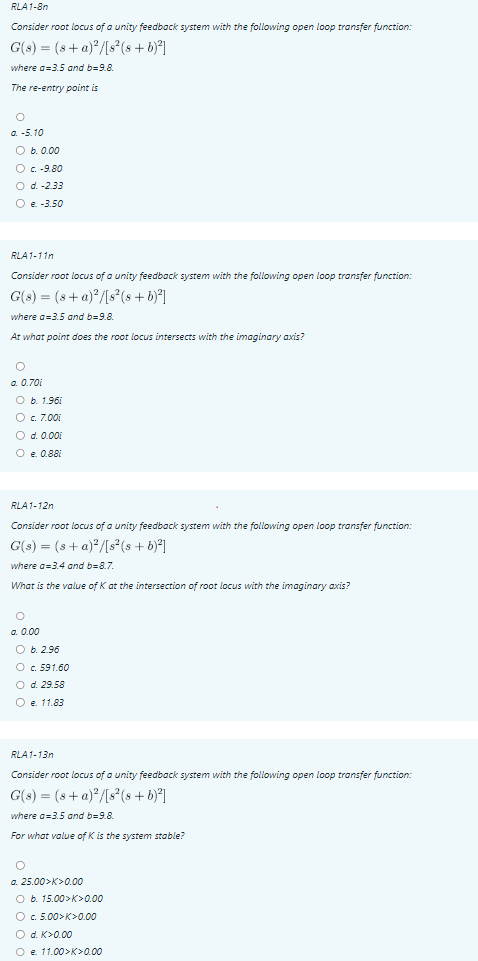
RLAT-8n Consider root locus of a unity feedback system with the following open loop transfer function: \[ G(s)=(s+a)^{2} /\left[s^{2}(s+b)^{2}\right] \] where \( a=3.5 \) and \( b=9.8 \). The re-entry point is \[ \begin{array}{l} \text { 5.10 } \\ \text { b. } 0.00 \\ \text { c. }-9.80 \\ \text { d. }-2.33 \\ \text { e. }-3.50 \end{array} \] RLA1-11n Consider root locus of a unity feedback system with the following open loop transfer function: \[ G(s)=(s+a)^{2} /\left[s^{2}(s+b)^{2}\right] \] where \( a=3.5 \) and \( b=9.8 \). At what point does the root locus intersects with the imaginary axis? RLA1-12n Consider root locus of a unity feedback system with the following open loop transfer function: \[ G(s)=(s+a)^{2} /\left[s^{2}(s+b)^{2}\right] \] where \( a=3.4 \) and \( b=8.7 \). What is the value of \( K \) at the intersection of root locus with the imaginary axis? RLA1-13n Consider root locus of a unity feedbock system with the following open loop transfer function: \[ G(s)=(s+a)^{2} /\left[s^{2}(s+b)^{2}\right] \] where \( a=3.5 \) and \( b=9.8 \). For what value of \( K \) is the system stable? a. \( 25.00>K>0.00 \) b. \( 15.00>K>0.00 \) c. \( 5.00>K>0.00 \) d. \( K>0.00 \) e. \( 11.00>K>0.00 \)