(Solved): Question: Find a DFA equivalent to the following NFA. *Important: Please draw an actual diagram us ...

Expert Answer

---

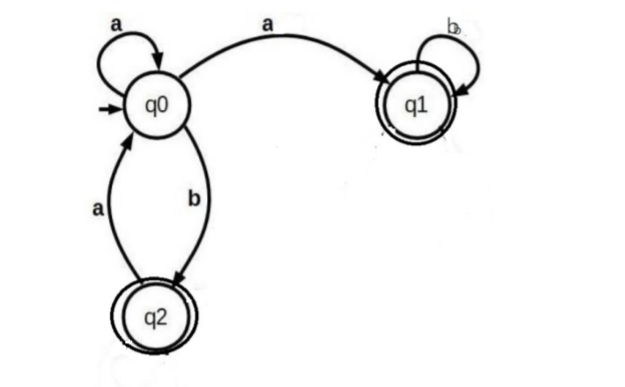
Step1:-

Here is the NFA:






To convert this NFA to an equivalent DFA, we can use the subset construction algorithm. The idea is to simulate the NFA starting from the initial state, and keeping track of all the states that we can reach by following epsilon transitions or by consuming input symbols. Each such set of states becomes a state in the DFA.

Here's the DFA that we get:






The initial state of the DFA is the set containing just the initial state of the NFA, which is {q1}. Since there are no epsilon transitions in the NFA, we don't need to worry about epsilon closures in the subset construction. For each input symbol a or b, we follow the transitions from each state in the current set, and collect all the states that we can reach. The resulting set becomes a state in the DFA, and we draw a transition from the current state to the new state labeled with the input symbol. We repeat this process for all input symbols and for all newly created states, until no more new states can be added.

The resulting DFA has 4 states, including the dead state ?. State {q2} is an accepting state, indicated by the asterisk.