(Solved): Quality Air Conditioning manufactures three home air conditioners: an economy model, a standard mod ...

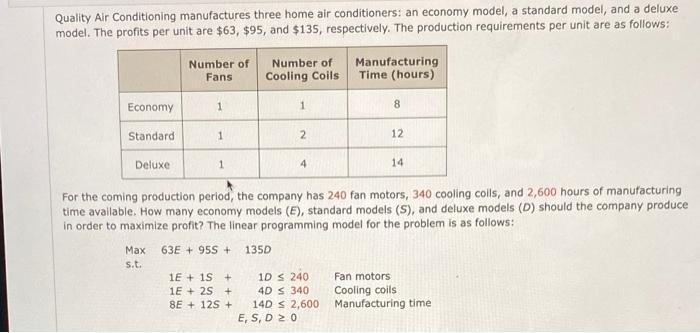
Quality Air Conditioning manufactures three home air conditioners: an economy model, a standard model, and a deluxe model. The profits per unit are \( \$ 63, \$ 95 \), and \( \$ 135 \), respectively. The production requirements per unit are as follows: For the coming production period, the company has 240 fan motors, 340 cooling colls, and 2,600 hours of manufacturing time available. How many economy models \( (E) \), standard models (S), and deluxe models (D) should the company produce in order to maximize profit? 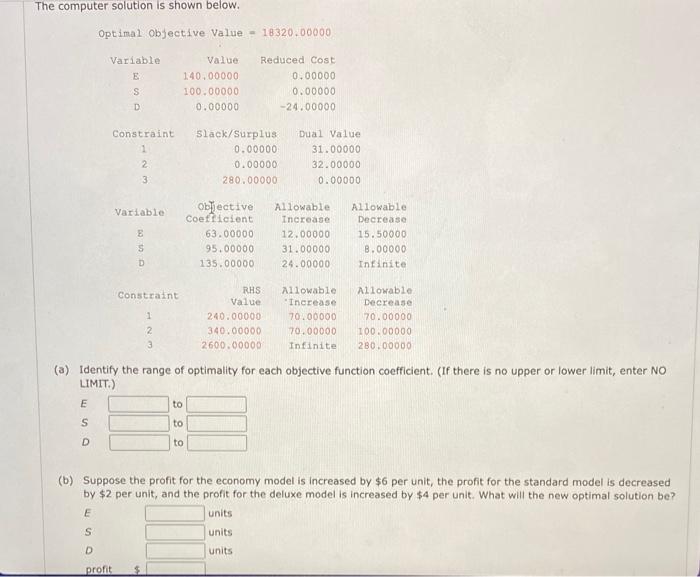The linear programming model for the problem is as follows: The computer solution is shown below. Optimal objective value \( =18320.00000 \) (a) Identify the range of optimality for each objective function coefficient. (If there is no upper or lower limit, enter NO LIMIT.) \( \begin{array}{ll}E & \text { to } \\ S & \text { to } \\ D & \text { to }\end{array} \) (b) Suppose the profit for the economy model is increased by \( \$ 6 \) per unit, the profit for the standard model is decreased by \( \$ 2 \) per unit, and the profit for the deluxe model is increased by \( \$ 4 \) per unit. What will the new optimal solution be? E units S units D units (c) Identify the range of feasibility for the right-hand-side values. (If there is no upper or lower limit, enter NO LIMIT.) \( \begin{array}{ll}\text { constraint } 1 & \text { to } \\ \text { constraint } 2 & \text { to } \\ \text { constraint } 3 & \text { to }\end{array} \) (d) If the number of fan motors available for production is increased by 90 , will the dual value for that constraint change? Explain. Yes, the dual value will change because 90 is greater than the allowable increase of 70 . Yes, the dual value will change because 90 is greater than the allowable increase of \( 12 . \)