(Solved): Poiseuille's Law According to a law discovered by the \( 19^{\text {th }} \)-century physician Pois ...

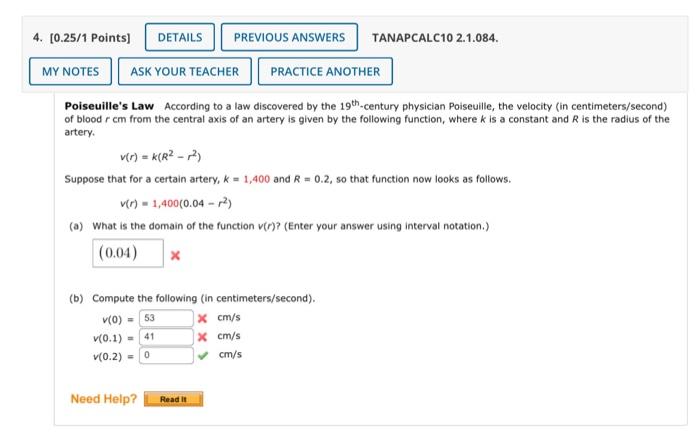
Poiseuille's Law According to a law discovered by the \( 19^{\text {th }} \)-century physician Poiseuille, the velocity (in centimeters/second) of blood \( r \mathrm{~cm} \) from the central axis of an artery is given by the following function, where \( k \) is a constant and \( R \) is the radius of the artery. \[ v(r)=k\left(R^{2}-r^{2}\right) \] Suppose that for a certain artery, \( k=1,400 \) and \( R=0.2 \), so that function now looks as follows. \[ v(r)=1,400\left(0.04-r^{2}\right) \] (a) What is the domain of the function \( v(r) \) ? (Enter your answer using interval notation.) (b) Compute the following (in centimeters/second). \[ \begin{aligned} v(0) &=& \times \mathrm{cm} / \mathrm{s} \\ v(0.1) &=& \times \mathrm{cm} / \mathrm{s} \\ v(0.2) &=& \checkmark \mathrm{cm} / \mathrm{s} \end{aligned} \]