(Solved): please help The American black bear (Ursus americanus) is one of eight bear species in the world. It ...

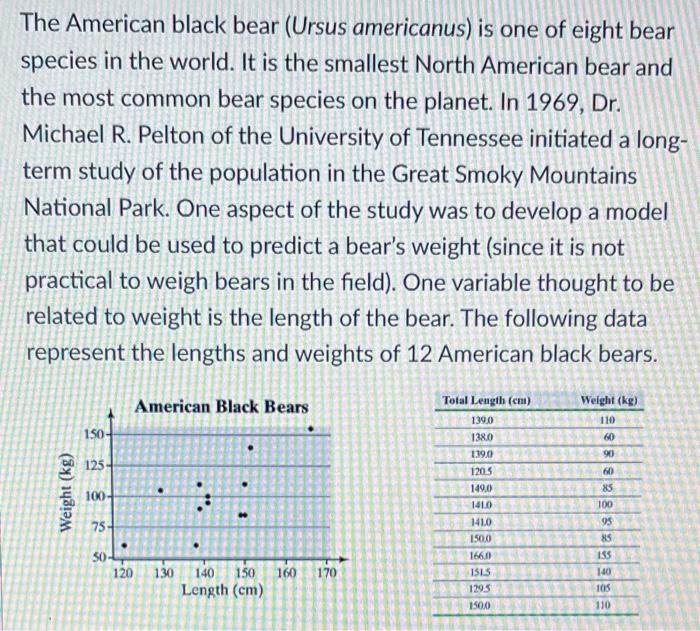
The American black bear (Ursus americanus) is one of eight bear species in the world. It is the smallest North American bear and the most common bear species on the planet. In 1969, Dr. Michael R. Pelton of the University of Tennessee initiated a longterm study of the population in the Great Smoky Mountains National Park. One aspect of the study was to develop a model that could be used to predict a bear's weight (since it is not practical to weigh bears in the field). One variable thought to be related to weight is the length of the bear. The following data represent the lengths and weights of 12 American black bears. 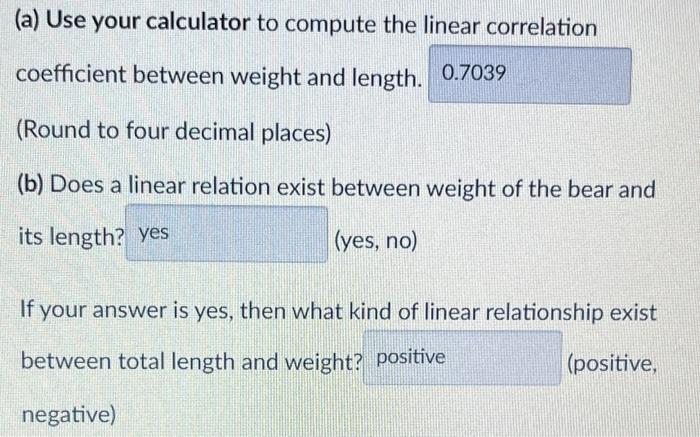(a) Use your calculator to compute the linear correlation coefficient between weight and length. (Round to four decimal places) (b) Does a linear relation exist between weight of the bear and its length? (yes, no) If your answer is yes, then what kind of linear relationship exist between total length and weight? (positive, negative) (c) Using your calculator, find the least-squares regression line treating total length as the explanatory variable and weight as the response variable. (Round the slope and \( y \)-intercept to three decimal places) Answer: \( \hat{y}= \) (d) Find the coefficient of determination? (Round your answer to four decimal places) (e) Suppose a 166.0-cm bear is captured in the field. Use the least-squares regression line you found above to predict the weight of the bear. What is the residual of the \( 166.0-\mathrm{cm} \) bear? Is this bear's weight above or below average for a bear of this length? 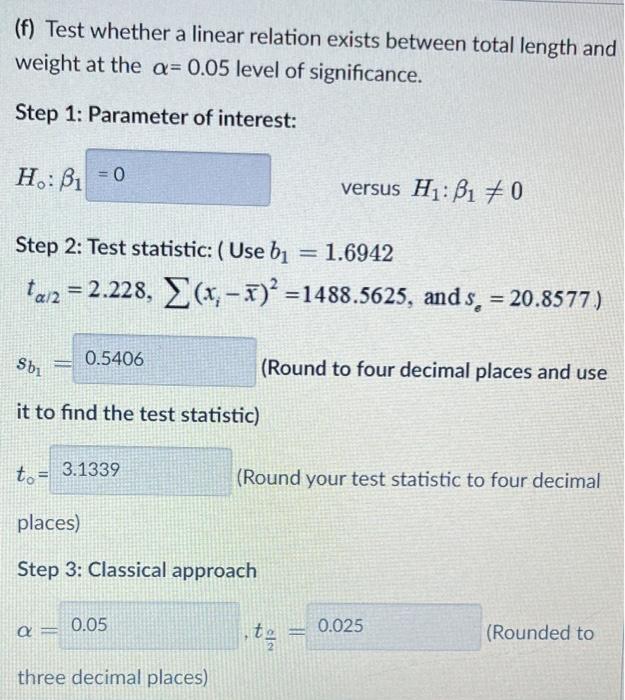(above, below) (f) Test whether a linear relation exists between total length and weight at the \( \alpha=0.05 \) level of significance. Step 1: Parameter of interest: \[ H_{0}: \beta_{1} \quad \text { versus } H_{1}: \beta_{1} \neq 0 \] Step 2: Test statistic: ( Use \( b_{1}=1.6942 \) \[ \left.t_{\alpha / 2}=2.228, \sum\left(x_{i}-\bar{x}\right)^{2}=1488.5625, \text { and } s_{e}=20.8577\right) \] \[ s_{b_{1}}= \] (Round to four decimal places and use it to find the test statistic) \[ t_{0}= \] (Round your test statistic to four decimal places) Step 3: Classical approach \[ \alpha=\quad, t_{\frac{\alpha}{2}}= \] (Rounded to three decimal places)