(Solved): please code problem #3 in jupyter notebook ^ Problem 1 Using NumPy 's linear algebra module, develo ...

please code problem #3 in jupyter notebook ^

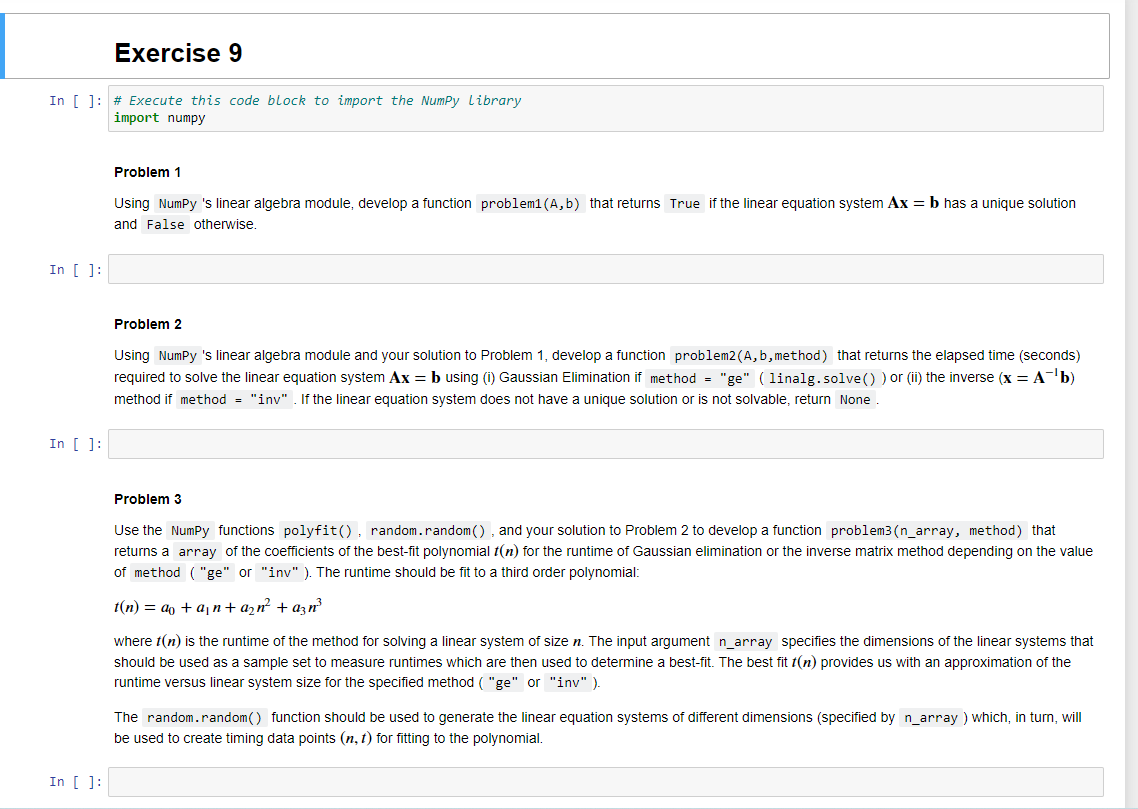
Problem 1 Using NumPy 's linear algebra module, develop a function problem1 ( \( A, b) \) that returns if the linear equation system \( \mathbf{A x}=\mathbf{b} \) has a unique solution and False otherwise. Problem 2 Using NumPy 's linear algebra module and your solution to Problem 1, develop a function problem2(A, b, method) that returns the elapsed time (seconds) required to solve the linear equation system \( \mathbf{A x}=\mathbf{b} \) using (i) Gaussian Elimination if method = "ge" ( linalg. solve()) or (ii) the inverse ( \( \mathbf{x}=\mathbf{A}^{-1} \mathbf{b} \) ) method if If the linear equation system does not have a unique solution or is not solvable, return Problem 3 Use the NumPy functions polyfit(), random.random(), and your solution to Problem 2 to develop a function problem3(n_array, method) that returns a array of the coefficients of the best-fit polynomial \( t(n) \) for the runtime of Gaussian elimination or the inverse matrix method depending on the value of method ("ge" or "inv"). The runtime should be fit to a third order polynomial: \( t(n)=a_{0}+a_{1} n+a_{2} n^{2}+a_{3} n^{3} \) where \( t(n) \) is the runtime of the method for solving a linear system of size \( n \). The input argument n_array specifies the dimensions of the linear systems that should be used as a sample set to measure runtimes which are then used to determine a best-fit. The best fit \( t \) ( \( n \) ) provides us with an approximation of the runtime versus linear system size for the specified method or The function should be used to generate the linear equation systems of different dimensions (specified by I which, in turn, will be used to create timing data points \( (n, t) \) for fitting to the polynomial.