(Solved): Periodic Interest Exercise The future value formula for compound interest. \[ F V=P V(1+i)^{n} \] D ...

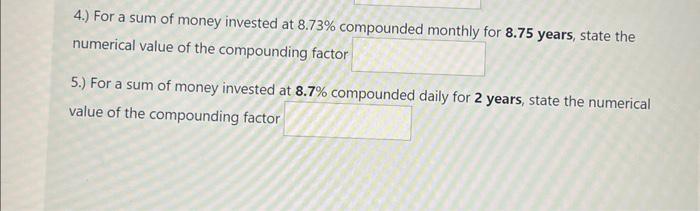
Periodic Interest Exercise The future value formula for compound interest. \[ F V=P V(1+i)^{n} \] Determining the periodic rate of interest. \[ \mathrm{i}=\frac{j}{m} \] Determining the number of compounding periods in the term of an investment or loan. \[ \mathrm{n}=\text { number of years in the term } \times \mathrm{m} \] Setting up the compounding factor \( (1+i)^{n} \) \( 7 \% \) per annum, compounded semi-annually for 15 years. \[ \begin{array}{l} j=0.07 \\ m=2 \\ i=0.07 / 2=0.035 \\ n=15 \times 2=30 \\ (1+i)^{n}=1.035^{30} \end{array} \] The numerical value \( =2.806793705 \) Provide all answers correct to 9 decimal places. 1.) For a sum of money invested at \( 4.6 \% \) compounded semi-annually for \( 5.5 \) years, state the numerical value of the compounding factor 2.) For a sum of money invested at \( 18 \% \) compounded daily for 3 years, state the numerical value of the compounding factor 3.) For a sum of money invested at \( 11 \% \) compounded semi-annually for 13 years, state the numerical value of the compounding factor numerical value of the compounding factor 5.) For a sum of money invested at \( \mathbf{8 . 7} \% \) compounded daily for \( \mathbf{2} \) years, state the numerical value of the compounding factor